Геологический толковый словарь

АНАЛИЗ ДИСКРИМИНАНТНЫЙ — аппарат для решения задач классификации. В общем виде задача классификации ставится следующим образом. Имеется k совокупностей π₁ π₂, . . ., π_k с функциями распределения F₁(x), F₂(x), . . ., F_k(x), которые определены полностью или с точностью до значений параметров. Наблюдение х, о котором заранее известно, что оно принадлежит к одной из этих совокупностей, должно быть отнесено к одной из совокупностей π₁ π₂, . . ., π_k с минимальной ошибкой. Обычно классификация происходит по нескольким признакам, т. е. рассматривается векторная случайная величина 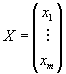. Функция наблюдений, которая применяется для классификации наблюдений, называется дискриминантной функцией. Дискриминантную функцию естественно выбирать так, чтобы ошибка классификации была минимальной. Если заданы две нормальные совокупности N(А_i, Λ), N (A₂, Λ), γде A_i — вектор математических ожиданий (i=l,2), Λ — матрица ковариационная , то дискриминантная функция Z имеет вид

Z = Х^τΛ^-1(A_i-A₂).

Здесь Х^τ— матрица транспонированная , Λ^-1 — обратная матрица. В случае различных ковариационных матриц Λ_i ≠ Λ₂ у распределений дискриминантная функция имеет вид

Z = (X-Ai)^τΛ_i^-1 (X-A_i)-(X-A₂)^τ Λ₂^-1 (X-A₂).

Если параметры распределений неизвестны, вместо них обычно подставляют соответствующие оценки по выборке . При классификации важно указать границу между совокупностями, называемую порогом. На практике ее часто устанавливают визуально. При реальных вычислениях А. д. применим во всех задачах, когда необходимо разделить наблюдения на два или несколько классов. Особенно широко распространен А. д. в петрологии, литологии и геохимии.