Геологический толковый словарь

СЛУЧАЙНЫЙ ПРОЦЕСС — функция 2-х аргументов X(t)= X(ω,t); 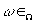— множество элементарных событий, 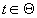— параметр, обычно интерпретируемый как время. Для каждого tX(ω,t) — функция только ω и представляет собой случайную величину. Для фиксированного ω X(ω,t) зависит только от t и есть функция одного вещественного аргумента; такая функция называется реализацией С. п., рассматривается либо как совокупность случайных величин, зависящих от параметра t, либо как совокупность реализаций процесса. Для определения С. п. 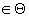надо знать вероятностную меру в функциональном пространстве его реализаций, напр., все конечномерные распределения F_t1,t2,…,tn(x₁,x_2,...,х_n) случайных векторов (x(t₁), x(t₂), ..., x(t_n)), t₁, t₂, ..., t_n удовлетворяющие условиям симметрии и согласованности. С. п. может быть непрерывным и дискретным, С. п. X (ω,t) непрерывен, если за малые промежутки времени лишь с малой вероятностью X (ω,t) может получить заметные по величине приращения. С. п.— дискретный, если X (ω,t) принимает не более чем счетное число значений за любой конечный промежуток времени. Рассматривают С. п. с непрерывным и дискретным временем с дискретным и непрерывным множеством состояний. Важную роль играет С. п. стационарный. В геологии и геохимии С. п. изучаются с 1949 г., но только в последние годы становится понятным их фундаментальное значение, так как они позволяют дать математическое представление процессов, протекающих в земной коре (Вистелиус, 1963; Пугачев, 1960).