Геологический толковый словарь

ЭНЕРГИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ — энергия (U), затрачиваемая на разрыв кристаллической решетки на ее составляющие с переносом на расстояние отсутствия взаимодействия, взятая с обратным знаком. Если решетка ионная, то это энергия разрыва на соответствующие ионы, если атомная или молекулярная, то это энергия разрыва на атомы, молекулы и т. д. Э. к. р. для молекулярных решеток это только небольшая часть энергии связей в решетке, так как связи атомов внутри молекул в нее не входят. Э. к. р. молекулярных решеток равна силам Ван-дер-Ваальса (см. Связь химическая ван-дер-ваальсова ). В настоящее время установлено, что абс. большинство природных соединений, в частности кислородные, не являются ионными, а в лучшем случае полуионными и полуковалентными. В связи с этим многие выводы, построенные на основе использования Э. к. р., рассчитывавшиеся обычно как ионные, имеют незначительную ценность. Существует ряд методов расчета Э. к. р. для бинарных соединений: по круговому процессу Борна — Габера, по формуле Борна — Ланде и упрощенным ее вариантам — формулам Капустинского и др. По круговому процессу U_i = Q + S + D + I — Е, где U_i — энергия решетки ионной; Q — теплота образования, S — теплота сублимации, D — энергия диссоциации, I — энергия ионизации и E — энергия сродства к электрону. По формуле Борна — Ланде 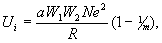где a — коэф. Маделунга, W₁ и W₂ — валентности ионов, R — межатомное расстояние, Ne²— произведение числа Авогадро на элементарный заряд электрона в квадрате, га — коэф. отталкивания электронных оболочек. В геол. науках обычно используют формулу Капустинского 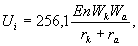где E_n — число структурных единиц. W_k и W_a — валентности катиона и аниона, r_k и r_a — их радиусы, или еще более упрощенную формулу Ферсмана U_i = 256,1 (ЕкА + ЕкВ + . . . + ЕкХ), имеющую универсальный характер по значениям Ек , слагающих соединения ионов, т. е. по энергетич. коэф. компон. расчета Э. к. р. Для атомных соединений круговой процесс упрощается: U_at = Q + S + D, для молекулярных: U_m = S (AB), где S (AB) — энергия сублимации молекул. 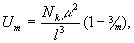Для теоретического расчета применяется формула где k — коэф., аналогичный коэф. Маделунга, µ — дипольный момент. Представление об Э. к. р. играет важную роль в геоэнергетическом анализе геохим. процессов, поэтому правильное использование этого понятия весьма важно. В. И. Лебедев.