Геологический толковый словарь

ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ — мера разброса значений случайной величины около математического ожидания . Согласно определению, Д. с. в. есть математическое ожидание квадрата разности между случайной величиной и ее математическим ожиданием:

DX=E(X-EX)²=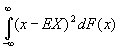

где F(x) — функция распределения случайной величины X. Полезна формула: DX = ЕХ² — (ЕХ)². Основные свойства Д. с. в. 1) D(cX) = C²DX, где с — постоянная; 2) D(X +У) = DX + DY, если X и У независимые случайные величины; 3) Dc = 0, если с — постоянная. Примеры. 1. Если X — равномерно распределенная в интервале (a, b) случайная величина, то Д. с. в. равна:

DX = .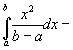

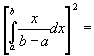
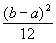2. Если X — случайная величина, распределенная по нормальному закону с плотностью

f(x)=,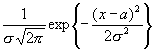

где а, σ — параметры распределения, то Д. с. в. в этом случае равна:

DX =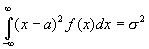

(см. Плотность распределения вероятностен). Выборочные оценки Д. с. в. широко используются во всех геол. дисциплинах, опирающихся па количественные характеристики. Аналогами Д. с. в. являются распространенные в литологии коэффициенты сортировки .