КРИТЕРИЙ
·χ2 — критерий значимости
для проверки по наблюденным частотам гипотезы относительно вероятностей.
Напр.: 1. Для проверки гипотезы о том,
что вероятности некоторых т событии равны соответственно заданным числам р1,
p2,...,
рm ,
вводится мера: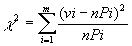 ,
где vi — наблюденное количество выборочных элементов,
принадлежащих i-му событию; n — объем выборки,
v1 + . . . + vm = п. Величина ·χ2 распределена асимпотически по закону ·χ2 с (n — 1) степенями свободы.
Если Р{χ2 >χ20} = α,
γде χ20 найдено по таблице при заданном α,
то проверяемая гипотеза отвергается на уровне значимости α. 2.
Для проверки независимости признаков A 1,
...,
As; В.,
. . .,
Вr вводят меру:
,
где vi — наблюденное количество выборочных элементов,
принадлежащих i-му событию; n — объем выборки,
v1 + . . . + vm = п. Величина ·χ2 распределена асимпотически по закону ·χ2 с (n — 1) степенями свободы.
Если Р{χ2 >χ20} = α,
γде χ20 найдено по таблице при заданном α,
то проверяемая гипотеза отвергается на уровне значимости α. 2.
Для проверки независимости признаков A 1,
...,
As; В.,
. . .,
Вr вводят меру: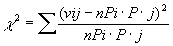 ,
где vij — количество наблюдений,
обладающих признаками Ai и bj,
pi = P(Ai); pj = P(Bj); εpj = εpj = 1; причем всего и независимых наблюдений,
χ2 распределена асимптотически по закону χ2 с (r — l)(s — 1) степенями свободы.
Вместо pi и рj можно поставить их оценки
по выборке
:
,
где vij — количество наблюдений,
обладающих признаками Ai и bj,
pi = P(Ai); pj = P(Bj); εpj = εpj = 1; причем всего и независимых наблюдений,
χ2 распределена асимптотически по закону χ2 с (r — l)(s — 1) степенями свободы.
Вместо pi и рj можно поставить их оценки
по выборке
: 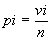 ,
,
 ,
где
,
где 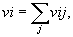
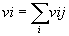 K.·χ2 широко применяется в геологии при проверке гипотез о согласии теоретической функции распределения с эмпирической,
а также для проверки наличия связи — последнее особенно важно при решении задач микроструктурного анализа.
K.·χ2 широко применяется в геологии при проверке гипотез о согласии теоретической функции распределения с эмпирической,
а также для проверки наличия связи — последнее особенно важно при решении задач микроструктурного анализа.
|

