МАТЕМАТИЧЕСКАЯ (АНАЛИТИЧЕСКАЯ) ГЕОЛОГИЯ
, Вистелиус,
1944,
1969,— научная дисциплина,
занимающаяся математическим моделированием геол. процессов и примыкающими к этому вопросу задачами.
Термин предложен в 1944 г. в русской лит.,
поддержан акад. В. И. Вернадским; в 1947 г. появился в англ. лит.
М. г. охватывает обширный круг вопросов,
делящихся по соотношению между геол. материалом и методом ввода в задачу математического аппарата на 3 раздела.
I — собственно математическая геология — ставит целью построение математических моделей геол.
процессов,
исходя из генетических представлений совр. геологии. Это необходимо для проверки непротиворечивости генетических построений геологии материалу наблюдений.
Анализ постановки вопросов происхождения тех или иных объектов в геологии показывает,
что интересны не столько частные,
конкретные объекты,
сколько представления о том,
как они возникают и формируются. Так как в геологии повторение явлений в фиксированных условиях невозможно,
то геолог вынужден строить заключение о процессе по единичным,
частным результатам этого процесса. Т. о.,
задачи геологии — задачи обратного типа. Изучение геол. объектов,
как порождений процессов,
показывает,
что ситуация,
в которой реализуется в природе процесс,
такова,
что точное предсказание свойств объектов невозможно. Поэтому исследуемые в геологии объекты,
как правило,
являются случайными величинами. Это значит,
что вероятностный подход к ее явлениям наиболее приемлем. Поэтому математические модели геол.
процессов являются вероятностными (стохастическими). В настоящее время осуществлено вероятностное моделирование ряда процессов: формирование слоистых структур,
последовательность образования зерен в гранитах,
активность кратера вулкана.
II — построение вероятностной модели процесса требует вполне конкретных представлений об особенностях процесса,
порождающего геол. объекты. Но генетические схемы геологии очень часто недостаточно конкретны для того,
чтобы построить стохастическую модель. В этом случае используются модели-отклики; это — функция,
описывающая основные свойства геол. объекта. Напр.,
многим осад. толщам свойственно циклическое строение,
но причины его не ясны. Т. о. для проверки тех или иных построений относительно свойств геол.
объекта необходимо иметь метод,
основанный на учете свойств этого объекта,
а не механизма его образования. В этом случае задача решается введением функции,
параметры которой оцениваются наблюдениями,
а вид задается представлениями о специфике свойств объекта. Если наши представления о свойствах объекта адэкватны действительности,
то найденные из опыта оценки параметров выявят свойства функции,
согласующиеся с проверяемой гипотезой; если же гипотеза не отражает свойств материала,
то оценки параметров дадут такие специфические черты функции,
которые укажут на несоответствие гипотезы материалу. Напр.,
мы хотим проверить гипотезу о том,
что на Дальнем Востоке количество К в мезозойских гранитоидах падает по направлению к Тихому океану.
Для этого вводится такая функция от географических координат,
линии ур. которой могут обрисовывать изменения в содер. К по направлению к океану.
Затем по данным наблюдений оцениваются параметры этой функции.
В зависимости от полученных оценок,
линии ур. функции (модели-отклика) укажут либо на снижение содер.
К к океану,
либо дадут узор,
не поддающийся геол. интерпретации. Последнее укажет,
что предлагаемая гипотеза не согласуется с наблюдениями в терминах данной модели-отклика.
Модели-отклики строились в литологии,
региональной геологии,
при подсчете запасов. В частности,
введение модели-отклика размещения концентраций Аu в конгломератах Рэнда (Ю.
Африка) позволило Криге и Матерому создать новый метод подсчета запасов.
III — использование в геологии математического аппарата с описательными целями.
Работы этого типа часто называют “статистической обработкой геол.
наблюдений”. В этом случае имеют место 2 типа исследований: 1) разумное сокращение информации; 2) проверка каких-либо гипотез при постулированных математ.
св. обрабат. материала.
При сокращении информации используется следующая идея. Мы имеем множество наблюдений и не можем по ним составить мнение о некоторых характеристиках изучаемого объекта.
Пожертвуем частью информации,
но зато рельефно представим интересующее нас свойство. Напр.,
нас интересует,
насколько велик разброс наблюдений. Ясно,
что наиболее полная информация дается всеми наблюдениями Но это неудобно.
Для удобства можно взять самое большое и самое малое наблюденные значения.
Это рельефно покажет разброс,
хотя часть информации и будет потеряна. Проверка гипотез,
осуществляемая с помощью описательной статистики,
может быть выяснена проще всего на примере. Допустим,
имеются м-ния А со средним содер. металла 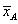 и соответственно м-ния В с
и соответственно м-ния В с 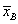 .
Необходимо проверить гипотезу о равенстве средних
.
Необходимо проверить гипотезу о равенстве средних 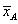 и
и 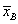 .
Для решения этой задачи средствами описательной статистики необходимо знать точные значения средних квадратичных отклонений σ2A и σ2В и число наблюдений.
На практике ни σ2A,
ни σ2 не известны; из наблюдений известны только их опытные аналоги — S2A и S2B.
Практик,
пользуясь общеизвестными формулами,
допускает,
что σ2A = S2A и σ2В = S2B.
Для точного решения задачи необходимо,
чтобы концентрации металла в пробах были независимы и распределены по нормальному закону (см. Распределение нормальное
). В этом случае можно вынести ответственное суждение — равны средние или нет.
Но при описательном применении статистики большая часть указаний аксиоматики опускается и счет ведется по готовым формулам.
В этом случае,
если аксиоматика,
положенная в основу метода,
совпадает с тем,
что наблюдается в природе,
то результат получается реальный,
если же аксиоматика не отвечает соотношениям,
существующим в природе,
то результат оказывается фиктивным. Т. о.,
эти методы не допускают механического применения. Напр.,
коэф. корреляции —
очень полезен во многих задачах геохимии,
минералогии,
петрологии,
палеонтологии и т. п.,
но было бы грубой ошибкой использовать его для выяснения связи между структурными поверхностями при анализе тект.
поднятий.
.
Для решения этой задачи средствами описательной статистики необходимо знать точные значения средних квадратичных отклонений σ2A и σ2В и число наблюдений.
На практике ни σ2A,
ни σ2 не известны; из наблюдений известны только их опытные аналоги — S2A и S2B.
Практик,
пользуясь общеизвестными формулами,
допускает,
что σ2A = S2A и σ2В = S2B.
Для точного решения задачи необходимо,
чтобы концентрации металла в пробах были независимы и распределены по нормальному закону (см. Распределение нормальное
). В этом случае можно вынести ответственное суждение — равны средние или нет.
Но при описательном применении статистики большая часть указаний аксиоматики опускается и счет ведется по готовым формулам.
В этом случае,
если аксиоматика,
положенная в основу метода,
совпадает с тем,
что наблюдается в природе,
то результат получается реальный,
если же аксиоматика не отвечает соотношениям,
существующим в природе,
то результат оказывается фиктивным. Т. о.,
эти методы не допускают механического применения. Напр.,
коэф. корреляции —
очень полезен во многих задачах геохимии,
минералогии,
петрологии,
палеонтологии и т. п.,
но было бы грубой ошибкой использовать его для выяснения связи между структурными поверхностями при анализе тект.
поднятий.
Если сравнивать положение математики в задачах каждого из выделенных разделов математической геологии,
то в I разделе представления о геол. процессе целиком определяют математические построения,
математика целиком подчинена геологии. Во II разделе геология определяет выбор функции.
Наконец,
в задачах III раздела асе основывается на априорном признании геологом уместности использования готового аппарата и соответствии его решаемым задачам.
Л. В. Вистелиус.
|

