МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
случайной величины есть ее числовая характеристика.
Если случайная величина X имеет функцию распределения F(x),
то ее М. о. будет: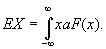
.
Если распределение X дискретно,
то М.о.: 
,
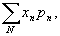где x1,
х2,
... — возможные значения дискретной случайной величины X; p1,
p2,
...— соответствующие им вероятности; n — пробегает некоторое множество индексов N.
М. о. может не существовать,
если ряд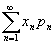 
расходится.
Напр.,
если хп = п,
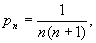n = 1,2,..., то 
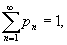а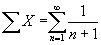 
.
Если X — непрерывная случайная величина с плотностью распределения f (х),
то 
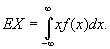Основные свойства М.
о.: 1) Еc = с,
если с —
постоянная величина; 2) Е(Х + У) = ЕХ + ХУ,
где X,
У — случайные величины; 3) Е(ХУ) = ЕХ ·ЕУ,
если X,
У — независимые случайные величины. На практике пользуются оценкой
.
М. о.,
называемой выборочным средним. Правильность определения оценки М.
о. имеет большое значение,
особенно при подсчете запасов.
|
