Геологический толковый словарь

МОМЕНТ К- ого порядка случайной величины X относит. точки α — есть математическое ожидание величины (X — α)^к: М_к(α) = Е(Х — α)^к. Если α=0, то М называется начальным, если α=EX≠0, то М. называется центральным. Начальный М.. первого порядка — есть математическое ожидание. Центральный М. первого порядка равен нулю. Центральный М. второго порядка есть дисперсия. Для М. суммы независимых слагаемых X и Y верно:

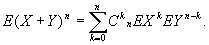Соответственно определяются выборочные М.—начальные: 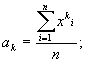центральные: 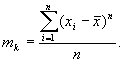Выборочные М. асимптотически нормальны. В геол. приложениях вычисление выборочных М. порядка выше четырех практически невозможно из-за быстрого роста ошибок. Первый выборочный М. в геохимии называется кларком; корень из второго момента в литологии получил название коэф. сортировки. М. третьего порядка очень важны для оценки специфики геохим. процессов.