Химическая энциклопедия

ЭКСЕРГЕТЙЧЕСКИЙ АНАЛИЗ , метод термодинамич. анализа пром. систем (в т. ч. хим.-технол. систем, ХТС), рассматриваемых во взаимод. с окружающей средой.
Связи, устанавливаемые при Э. а. между термодинамич. характеристиками и техн.-экономич. показателями анализируемой системы, дают возможность оценить эффективность ее работы, а также определить пути и способы совершенствования. Объективность получаемых при таком анализе оценок обусловлена прежде всего тем, что они основаны на расчете минимально необходимых материальных и энергетич. затрат на реализацию исследуемого технол. процесса. В большинстве др. методов для этих целей используют нек-рые операции сравнения (напр., изменения энтропии системы), по отношению к к-рым и оцениваются показатели изучаемого объекта; результаты подобного анализа, естественно, зависят от удачного выбора операций сравнения. Э. а. избавляет исследователя от необходимости подбора указанных операций для действующих установок, а для новых (проектируемых) позволяет сразу выявить возможность их внедрения в произ-во путем сопоставления минимально требуемых затрат с имеющимися в наличии ресурсами. Э. а. успешно используют в отраслях хим.-лесного комплекса (напр., в произ-вах метанола, HNO₃), металлургии, криогенной технике и др., причем все шире для повышения экономичности высокоэнергоемких процессов и произ-в.

Некоторые основные понятия. В основе Э. а. лежит понятие эксергии (от греч. ех- - приставка, означающая здесь высокую степень, и ergon - работа). Существует неск. ее формулировок. По одной из них (3. Рант, 1956) эксергия суть работоспособность- термин, применяемый для обозначения макс. работы, к-рую может совершить система при переходе из данного состояния в состояние равновесия со всеми компонентами окружающей среды, рассматриваемой как источник и приемник любых потоков энергоносителей (вода, пар, сырье, напр. нефть, хим. продукты) и энергии (электрическая, тепловая).
Поясним данное определение. Во-первых, макс. работу можно получить только в обратимом (равновесном) процессе, к-рый теоретически возможен при бесконечно малой движущей силе (напр., разности т-р, давлений, хим. потенциалов). Все реальные процессы происходят с возрастанием энтропии (см., напр., Второе начало термодинамики )при конечной разности т-р и, следовательно, необратимы. Поэтому полученная в них работа всегда будет меньше максимально возможной; для оценки этой работы ее надо сравнивать с максимально возможной в данном процессе, т. е. с эксергией. Во-вторых, макс. работа м. б. получена только при взаимод. системы с окружающей средой. Напр., для получения эксергии топлива его сжигают в определенном кол-ве О₂, взятом из окружающей среды; при использовании для горения чистого кислорода будет получено больше теплоты, но суммарная эксергия окажется меньше, т. к. для получения О₂ из воздуха необходимо затратить нек-рую работу, а значит, эксергию. Аналогично при нагревании к.-л. тела теплоту нужно подводить только для повышения его т-ры выше т-ры окружающей среды, а до этой т-ры подогрев происходит за счет теплоты, отбираемой от среды.
В основе одной из иных формулировок эксергии (З. Рант, 1962) лежит (для случаев, когда начальная т-ра тела выше т-ры окружающей среды) допущение о том, что энергию тела можно представить суммой двух составляющих: Э = Е + А. В соответствии с этим равенством эксергия Е определяется как часть энергии, к-рая в данных условиях окружающей среды м. б. превращена в любую др. ее форму (см. ниже). Вторую составляющую А, наз. анергией (от греч. "а" - отрицат. частица и ergon - работа), ни в какую иную форму энергии, включая мех. работу, превратить нельзя; между анергией и энтропией существует связь: анергия - энергия полностью неорганизов. движения молекул, энтропия - мера этого движения.
Наиб. наглядно эксергию (и анергию) можно представить графически. На рис. 1 изображен произвольный процесс 1-2, в к-ром теплота сообщается нек-рому рабочему телу. Эксер-гия теплоты Е_т измеряется заштрихованной площадью. Неработоспособной части теплоты, т. е. анергии, отвечает площадь под линией Т₀ = const, равная произведению T₀(S₁- S₂), где Т₀ - т-ра окружающей среды; S_lи S₂ - энтропия системы в начале и конце процесса.
Эксергия измеряется в тех же единицах, что и энергия и работа,- в Дж, эксергия потока в-ва - в Вт, потока теплоты - в Дж/с. Таким образом, эксергия, характеризуя качество энергии пром. системы, т. е. способность быть превращенной в полезную работу, является универсальной мерой энергетич. ресурсов.

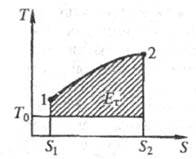
Рис. 1. Графическое изображение эксергии.

Параметры окружающей среды не зависят от параметров рассматриваемой системы, обычно предполагаются постоянными и, согласно указанному определению эксергии, должны находиться в термодинамич. равновесии с параметрами системы. Однако, строго говоря, это условие невыполнимо, поскольку в среде всегда существуют градиенты т-р, давлений и хим. потенциалов (что в практич. расчетах можно не учитывать). Для полной характеристики среды достаточно знать не более трех параметров (как правило, т-ру, давление, хим. состав). До тех пор пока все параметры системы не сравняются с соответствующими параметрами среды, равновесие не будет достигнуто и система может производить определенную работу, т. е. обладает эксергией. При Э. а. работы пром. установок в качестве окружающей среды принимают атм. воздух. Из самого понятия "эксергия" следует, что эксергия окружающей среды равна нулю.

Виды и составляющие эксергии. Различают два гл. ее вида: эксергию таких форм энергии, к-рые не определяются энтропией, и эксергию потоков в-ва и энергии, характеризуемых энтропией. К первым относятся мех., электрич., электромагн. и иные виды энергии; в данном случае эксергия равна энергии системы и никаких спец. расчетов для определения Е не требуется. Ко вторым принадлежат формы энергии (напр., внутр. энергия в-ва, энергия хим. связей, теплового потока), для каждой из к-рых эксергию вычисляют индивидуально в зависимости от наличия и вида ее материального носителя -разл. тел [эксергия в-ва (массы) в объеме либо потоке] или объектов, не связанных с массой в кол-вах, подлежащих учету (эксергия теплового потока). Эксергия потока в-ва включает термомех. и хим. составляющие, обусловленные различием термич. и мех. параметров в-ва и окружающей среды и соответствующих хим. состава и хим. потенциалов.

Расчет эксергии. Эксергия в-ва в замкнутом объеме с термодинамич. параметрами U, S, Т, р и V определяется соотношением:

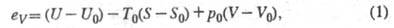
где e_V - удельная (на единицу массы) эксергия в-ва; U_c, S₀, T₀, p₀, V₀ - внутр. энергия, энтропия, т-ра, давление и объем в-ва при полном равновесии анализируемой системы с окружающей средой. Ф-ла (1) выражает эксергию в-ва в замкнутом объеме в процессе, завершающимся выравниванием соответствующих параметров системы и среды. При расчетах эксергии рабочего тела (носителя эксергии) в замкнутой системе в двух разных состояниях ур-ние (1) приводится к виду:

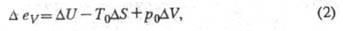
где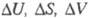 - изменения параметров в-ва при переходе из одного состояния в другое.
Необходимость определения эксергии в замкнутом объеме возникает чаще всего при расчетах периодич. процессов и установок периодич. действия, в к-рых рабочее тело не выходит за пределы данной системы. Однако на практике большинство хим.-технол. процессов непрерывны, стационарны и сопровождаются перемещениями материальных и энергетич. потоков. Поэтому такие задачи связаны с определением эксергии в-ва в потоке. Ее термомех. составляющую находят по ф-ле:

q - переносимый в-вом уд. тепловой поток; S - энтропия в-ва в потоке.
Для идеальных газов термомех. эксергия определяется выражением:

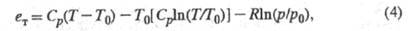
где С_р - уд. теплоемкость в-ва; р и Т - давление и т-ра в-ва в потоке; R - газовая постоянная.
Хим. составляющую эксергии (хим. эксергию), связанную с термодинамич. параметрами хим. р-ции, рассчитывают, используя разл. полуэмпирич. соотношения. Так, для газов и жидкостей установлены соотношения между их хим. эксергией и высшей теплотой сгорания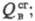 напр., в процессах выпаривания, ректификации и сушки хим. эксергию топлива находят по ф-ле:

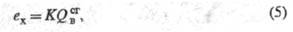
где коэф. К равен 0,975 (газы) и 0,95 (жидкости), если в молекуле в-ва содержится более одного атома С. Для др. в-в, напр. газов, можно принять след. значения К: 0,97 (генераторный газ), 0,98 (колошниковый газ), 1,0 (коксовый газ), 1,04 (прир. газ).
В случае твердых топлив с учетом влагосодержания W хим. эксергию можно с достаточной для практич. целей точностью принять равной их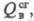 т. е.

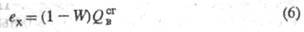
Т-ра топлив обычно близка к т-ре окружающей среды, поэтому необходимость принимать во внимание в расчетах их термомех. эксергию не возникает; исключение составляет тяжелое жидкое топливо (мазут), к-рое для снижения его вязкости, как правило, подогревают до 70-100 °С.
Эксергия теплового потока. Функционирование ХТС в той или иной степени обусловлено обменом энергией с окружающей средой. При передаче от одного тела к другому и к среде Энергии в форме теплового потока (теплопроводность) вместе с ним сообщается и определенное кол-во эксергии. Если приемником теплоты служит окружающая среда с т-рой T₀, уд. эксергия теплового потока, имеющего т-ру Т, составляет:

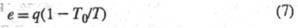
Величина (1 - T₀/T) = Т_в наз. эксергетической температурой. При Т<Т₀направления потоков противоположны: тепловой движется от окружающей среды (отрицателен), эксергетический - всегда к среде (положителен).
Во мн. хим.-технол. системах, особенно высокотемпературных, существ. роль играет обмен энергией в форме излучения с др. объектами и средой. Эксергию излучения находят по ф-ле:

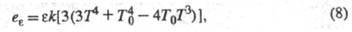
где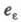- уд. эксергия, приходящаяся на единицу площади излучающей пов-сти;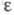 и Т - степень ее черноты и т-ра; Т₀ -т-ра окружающей среды; k - постоянная Больцмана.
Эксергия влажного воздуха. В практич. приложениях Э. а. важное значение имеет вычисление эксергии влажного воздуха, что обусловлено его применением в качестве рабочего тела во мн. процессах хим. технологии (напр., при сушке ). В данном случае особенность определения эксергии состоит в том, что началом отсчета служит переменное состояние воздуха в окружающей среде. Для удобства расчетов влажный воздух принято условно рассматривать как смесь 1 кг абсолютно сухого воздуха и X кг водяных паров. Соотв. эксергия такой смеси е_1+X, отнесенная к 1 кг абсолютно сухого воздуха, будет равна сумме эксергий воздуха и паров и рассчитывается по ф-ле:

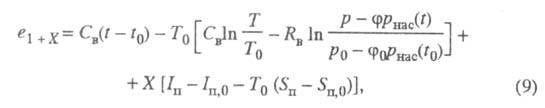
где С_в и R_B - теплоемкость и газовая постоянная сухого воздуха; t и t₀, Т и Т₀ - т-ры анализируемого потока и окружающей среды соотв. в °С и К;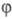 и р и р₀ - относит. влажности воздуха и полные давления в потоке и среде; p_наc(t) и p_наc(t₀) - давления насыщенных водяных паров при т-рах потока и среды; I_п и S_п, I_п,0 и S_п,0 - энтальпии и энтропии паров при параметрах потока и среды. Изменения состояния окружающей среды влияют на величину зксергии, поэтому, чтобы избежать ошибок в ее расчете, нужно учитывать не фиксированные, а реальные параметры среды.
Расчет по ф-ле (9) эксергий влажного воздуха при разл. параметрах требует значит. затрат времени. Для их сокращения часто применяют графоаналит. способ на основе спец. номограммы. Найденные по ней параметры подставляют в упрощенную ф-лу:

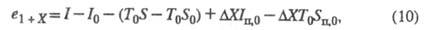
где дельтаХ= X— Х₀ (Х₀ - влагосодержание среды). Расхождение в результатах расчета этим способом и по ф-ле (9) не превышает 3-5%.

Эксергетический баланс. С помощью основных соотношений [ф-лы (1)-(10)] для определения эксергетич. показателей эффективности работы ХТС составляют их эксергетич. балансы. Для любой реальной системы такой баланс представляет собой сопоставление всех эксергетич. потоков на входе (Е) и выходе (E") из нее с учетом затрат эксергий на компенсацию внутр. и внеш. потерь и м. б. выражен в виде:

где- потери эксергий в системе.
Внутр. потери обусловлены необратимостью протекающих в ХТС процессах (гидравлич. сопротивления, тепло- и массообмен и др.); внешние - потерями эксергий через тепловую изоляцию, с выходящими из системы потоками (напр., нагретая вода, отработанные газы). Если выполненные на основе эксергетич. баланса системы или ее отдельных элементов расчеты показывают отсутствие E^п в них, это свидетельствует об ошибках в определении параметров действующих ХТС либо о невозможности ее реализации для проектируемых произ-в. Эксергетич. потери находят по ф-ле Гюи - Стодоли:

где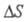- изменение энтропии системы.
Эксергетические диаграммы. Весьма полезны и достаточно информативны для анализа эффективности функционирования ХТС эксергетич. диаграммы, или диаграммы Грассмана, на к-рых потоки эксергий в системе изображены в определенном масштабе по "ширине", пропорциональной их численным значениям. Диаграммы наглядно показывают потери эксэргии в системе, места их появления и перераспределения между элементами данного объекта. На рис. 2 приведена такая диаграмма для ХТС с двумя входными материальными потоками, к-рым отвечают эксергий Е₁ и Е₂. В результате взаимод. этих потоков на выходе из системы получают целевые продукты с эксергиям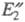ии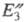и побочный продукт с эксергией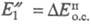 . Сумма 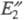+ 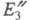меньше суммарной эксергий входных потоков на величину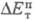(обусловлены необратимостью тепло- и массообмена в системе) и внеш. потерь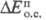 в окружающую среду.

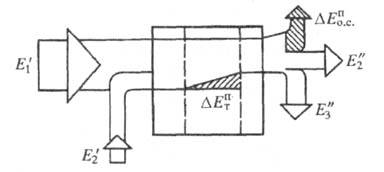
Рис. 2. Диаграмма Грассмана для ХТС с двумя входными материальными потоками.

Эксергетический кпд системы. Диаграммы Грассмана и непосредственно эксергетич. баланс в форме ур-ния позволяют найти количеств, показатели эффективности работы анализируемой ХТС. Среди этих показателей наиб. распространен эксергетич. кпд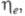 определяемый соотношением:

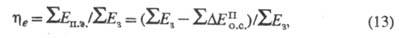
где - сумма потоков эксергий, отражающая полезный эффект от функционирования системы;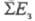- полные затраты эксергий на достижение заданного эффекта.
Для идеального, полностью обратимого процесса, в к-ром потери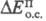 отсутствуют,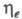= 1; если подведенная эксергия полностью теряется в процессе, то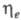= 0. В реальных процессах всегда соблюдается неравенство: 0 <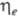< 1; при этом чем выше численное значение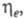 тем термодинамически совершеннее система. Из ф-лы (13) следует также, что разность между эксергиями, обусловливающими полезный эффект и эксергетич. затраты, всегда равна суммарной потере эксергий от необратимости протекающих в системе процессов.
Т. обр., эксергетич. кпд носит обобщенный характер. Конкретное выражение для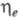 зависит от назначения и особенностей анализируемого процесса и видов взаимод. потоков. Напр., с использованием понятия "транзитной" эксергий E^тр (количественно в системе не изменяется) ур-ние для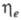 принимает форму:

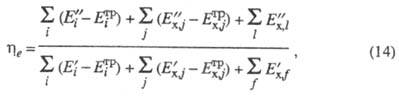
где ниж. индексы обозначают: i - все виды эксергии, кроме химической; х - хим. эксергия; j - компоненты в-ва, одновременно присутствующие во входном и выходном потоках; l - новые в-ва, образующиеся в системе; f - в-ва, полностью превращающиеся в др. в-ва.
Объем, качество и ценность информации, получаемой на основе эксергетич. баланса ХТС, проиллюстрируем двумя примерами из опыта использования Э. а. в хим. технологии.
I. Анализ узла синтеза NH₃ в технол. схеме его произ-ва показал, что макс. потери эксергий происходят в колонне синтеза и уменьшить их можно: 1) на 15-18% без значит. изменения технол. процесса; 2) с принципиальным изменением режима синтеза NH₃ (напр., повышением т-ры в одной из зон колонны), что позволило бы квалифицированнее использовать теплоту р-ции и выдавать на сторону пар более высоких параметров.
II. Для оценки эффективности работы типовой пневматич. сушилки (трубы-сушилки) применительно к сушке конкретного продукта наряду с обычным анализом на основе материального и теплового балансов установки (рис. 3) проведен ее Э. а. В соответствии со схемой материальных (G), тепловых (Q) и эксергетич. (Е)потоков был составлен эксергетич. баланс:

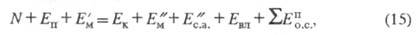
где N - мощность двигателя вентилятора; Е_п - эксергия пара; Е_к - эксергия образующегося в калорифере конденсата;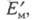 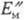- эксергия влажного материала на входе в установку и высушенного материала;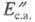- эксергия сушильного агента на выходе из установки; Е_вл - эксергия испаренной влаги; Е^п -суммарные потери эксергии в установке. Остальные обозначения эксергетич. 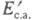потоков на схеме: Е_в - эксергия воздуха, поступающего в вентилятор и калорифер;- эксергия сушильного агента на входе в сушилку; Е_под - эксергия подсасываемого наружного воздуха;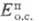- потери эксергии в окружающую среду с отработанным сушильным агентом.

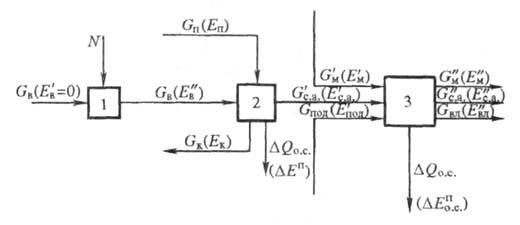
Рис. 3. Схема потоков в сушильной установке: 1 - вентилятор; 2 - калорифер; 3 - сушилка.

Эксергии материальных потоков в составе эксергетич. баланса рассчитаны по представленным ранее ф-лам. Потери эксергии выражены суммой потерь в отдельных аппаратах и вычислены по ф-ле Гюи-Стодоли (определение возможно также по разности эксергии материальных и энергетич. потоков на входе и выходе из соответствующих аппаратов, если нет необходимости в детализации этих потерь). Результаты расчетов показали, что полезные затраты эксергии на испарение влаги из материала незначительны по сравнению с располагаемой эксергией греющего пара; основные потери эксергии выявлены в калорифере.
Сопоставлением эксергетич. баланса с тепловым балансом этой установки найдено, что в последнем уд. вес аналогичных статей расхода существенно отличается от полученных при эксергетич. расчете значений. Так, потери в окружающую среду в тепловом балансе составили 60,4%, а в эксергетическом - 15,9% (суммарные потери в калорифере и сушилке, из к-рых отработанный сушильный агент выбрасывается в атмосферу). Это объясняется низким энергетич. потенциалом уходящих газов, что, естественно, сказалось на численном значении их эксергии. Что касается таких статей расхода, как потери в калорифере, при смешении паров влаги с сушильным агентом, от гидравлич. сопротивления установки и от необратимости тепло- и массообмена, то они вообще не нашли отражения в тепловом балансе. Т. обр., в сопоставлении с ним эксергетич. баланс полнее и объективнее отразил все энергетич. затраты на реализацию сушильного процесса и позволил выявить "узкие" места в нем. В данном случае повышение эффективности работы установки в первую очередь было связано с совершенствованием функционирования калорифера (изменены конструкция и параметры работы, в частности, снижено давление греющего пара).

Структурные коэффициенты. При Э. а. ХТС существенна связь их общих показателей с характеристиками отдельных элементов (аппаратов). Меру влияния отдельного элемента на эффективность работы системы в целом принято оценивать с помощью т. наз. структурного коэф.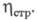 Он представляет собой отношение изменения к.-л. эксергетич. параметра всей системы (кпд, потери, входные и выходные потоки) к его изменению в одном из элементов; при этом все остальные параметры системы считаются неизменными.
Оптим. оценки функционирования ХТС получены при вычислении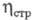 через эксергетич. кпд. Расчетные соотношения для этого коэф. зависят от структурных связей в системе, т. е. от наличия последовательно, параллельно или смешанно соединенных между собой ее элементов. Анализ показывает, что в ХТС с последоват. соединением аппаратов одинаковые изменения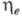 к.-л. элемента в равной степени отражаются на величине данного коэф. для всей системы независимо от места расположения в ней аппарата. В то же время изменение потерь эксергии зависит от размещения элемента: чем дальше от входа в систему он находится, тем сильнее влияние указанных потерь на работу системы. Поэтому необходимо обращать особое внимание на уменьшение эксергетич. потерь на заключит. стадиях процесса, протекающего в ХТС с таким соединением элементов.
В системах с параллельным соединением элементов изменение потерь эксергии в любом аппарате вызывает эквивалентные изменения потерь во всей ХТС. Э. а. с помощью структурных коэф. реальных пром. систем требует их предварит. преобразования в схемы, состоящие из параллельно соединенных участков, в к-рых аппараты связаны последовательно.

Оптимизация работы ХТС на основе Э. а. осуществляется с помощью целевых ф-ций (см. Оптимизация );обычно применяют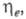 приведенные денежные затраты на единицу эксергии продукта, сумму уд. затрат эксергии. На практике широко используют вторую из перечисленных ф-ций. В общем виде показатель, служащий для нахождения оптим. параметров ХТС на основе данной целевой ф-ции, имеет вид:

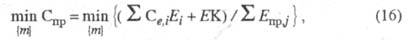
где С_е,i и С_пр - стоимость единицы эксергии сырья и продукции; E_i и E_{прj -} их эксергии; К - капитальные затраты; {т} -совокупность параметров, по к-рым оптимизируется работа системы. Выражение (16) конкретизируется в зависимости от особенностей структуры ХТС и условий ее функционирования.
Весьма нагляден и эффективен графич. метод представления изменений оптимальных затрат на работу ХТС с помощью термоэкономич. диаграмм материальных и энергетич. потоков. На рис. 4 изображены такие диаграммы для выпарной установки, включающей ряд последовательно соединенных аппаратов (1,2, ..., N). При построении диаграмм затраты делятся на энергетические и неэнергетические. Энергетич. составляющие (потоки эксергии на входе в каждый аппарат и выходе из него; рис. 4, а)вычисляются через термодинамич. характеристики системы. По мере движения от ее входа к выходу из-за потерь эксергии в аппаратах общий эксергетич. поток уменьшается. Стоимость энергетич. затрат, полученную умножением "ширины" потока (рис. 4, а) на стоимость единицы эксергии, откладывают в выбранном масштабе на "стоимостной" диаграмме (рис. 4, б)ниже оси О-О ( ...,

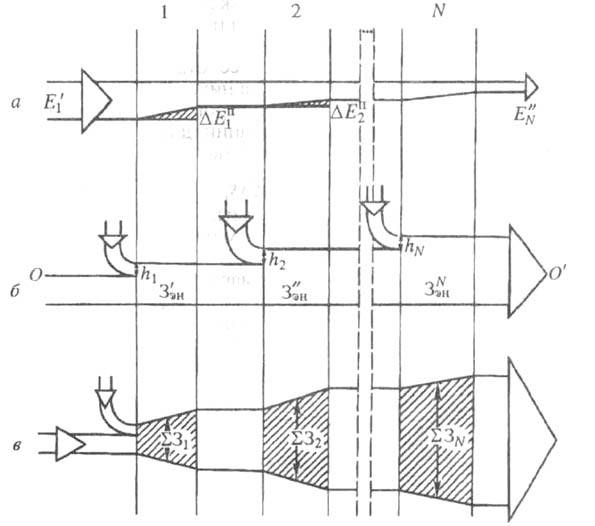
Рис. 4. Термоэкономические диаграммы для системы из последовательно соединенных аппаратов.

На той же диаграмме выше линии О-О откладывают стоимость неэнергетич. затрат, складывающихся из отчислений капиталовложений и трудовых затрат (на эксплуатацию аппаратов); эти затраты косвенно (через размеры аппаратов) также связаны с термодинамич. характеристиками системы.
В каждом аппарате неэнергетич. затраты растут скачком (h₁ h₂, ..., h_N) из-за дополнит. трудовых затрат.
Диаграмма на рис. 4, в - результирующая; она получается делением ширины потока на рис. 4, б на соответствующую ширину потока на диаграмме 4, а. Из рис. 4, в следует, что по мере движения потоков от входа системы к ее выходу неэнергетич. затраты увеличиваются быстрее, чем энергетические. Подобные ХТС довольно широко распространены в пром-сти.
В более общем случае энергетич. затраты, обусловленные промежут. вводами материальных или энергетич. потоков, приводят к количеств, изменению уд. затрат. Однако преимущественное возрастание неэнергетич. затрат типично и для таких ХТС, поскольку любые преобразования требуют создания соответствующего оборудования и одновременно не всегда связаны с дополнит. трудовыми затратами. Являясь целевой ф-цией при оптимизации работы ХТС, уд. стоимостные затраты позволяют также получить информацию и о тех ее элементах, к-рые в наиб. степени способствуют увеличению указанных затрат.

Лит.: Шаргут Я., Петела Р., Эксергия, пер. с польск., М., 1968; Сажин Б. С., Основы техники сушки, М., 1984, с. 283-309; Бродянский В.М., Фратшер В., Михалек К., Эксергетический метод и его приложения, М., 1988; Кутепов А. М., Бондарева Т. И., Беренгартен М.Г., Общая химическая технология, 2 изд., М., 1990, с. 27-45; Сажин Б. С., Булеков А. П., Эксергетический анализ в химической технологии, М., 1992.

Б. С. Сажин, А. П. Булеков.