Химическая энциклопедия

ГАЗЫ , в-ва в агрегатном состоянии, характеризующемся слабым взаимод. составляющих в-во частиц (по сравнению с их средней кинетич. энергией), в результате чего Г. заполняют весь предоставленный им объем. Г., как и нормальные (обычные) жидкости, макроскопически однородны и изотропны при отсутствии внеш. воздействий, в отличие от анизотропных состояний в-ва - твердого кристаллического и жидких кристаллов. Строго различать жидкое и газообразное состояния в-ва на фазовой диаграмме можно лишь при т-ре ниже критической Г_кр (см. рис.), т.к. выше Т_кр газ нельзя превратить в жидкость повышением давления. Ниже Ткр возможно фазовое равновесие жидкость — пар, причем газообразному состоянию отвечает фаза с меньшей плотностью (Г., находящийся в термодинамич. равновесии с жидкой или твердой фазой того же в-ва, обычно наз. паром). В критич. точке различие между жидкостью и паром исчезает, поэтому возможен непрерывный (без фазового превращения) переход из газообразного состояния в жидкое. При этом все св-ва в-ва меняются постепенно (наиб, быстро вблизи критич. точки). В тройной точке Т^ сосуществуют газ, жидкость и твердое тело (кристалл), причем плотность Г. вблизи тройной точки обычно на три порядка меньше плотности жидкости или кристалла. Кривую сосуществования жидкости и Г. наз. кривой парообразования, твердого тела и Г.-кривой сублимации (возгонки).

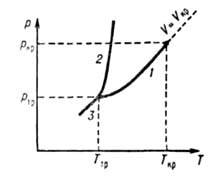
Диаграмма состояния однокомпонентной системы в координатах давление р-темпера-тура Т! Линии /, 2 и 3-кривые парообразования, плавления и возгонки соотв.; 7"_кр и р_кр-координаты критич. точки; Т_тр и р_тр -координаты тройной точки; И,—-Критич. объем.

В нормальных условиях (при 0°С и атм. давлении) в газообразном состоянии находятся элементы гелиевой группы (Не, Ne и т. д.), а также ряд элементов, образующих молекулярные газы: О₂, N₂, Н₂, Г₂ и С1₂. Атм. воздух состоит из N₂ и О₂ (соотв. 75,5 и 23,1% по массе), благородных газов, N₂O, CO₂ и паров Н₂О (остальные 1,4%). В природе Г. образуются как продукты жизнедеятельности бактерий, при превращениях орг. в-в, восстановлении минер. солей и др. В недрах Земли Г., в основном СН₄ и др. легкие углеводороды, как правило, сопутствуют нефтям; встречаются газовые месторождения, содержащие до 70% неуглеводородных компонентов (H₂S, CO₂ и" др.).

При низких давлениях Г. смешиваются друг с другом в любых соотношениях. При высоких давлениях и т-рах выше Т_кр взаимная р-римость Г. может быть ограниченной и возможно равновесное сосуществование двух газовых фаз; такие системы рассматривают как расслаивающиеся газовые р-ры (см. Критическое состояние ). Р-римость Г. в жидкостях и твердых телах может достигать больших значений (см. табл. 1).

Табл. 1.-РАСТВОРИМОСТЬ ГАЗОВ В ЖИДКОСТЯХ ПРИ 298 К И 10^s Па (в мольных долях)

Теория газообразного состояния. Важнейшая теоретич. модель газообразного состояния-ид сальный газ, для к-рого энергия взаимод. между молекулами пренебрежимо мала по сравнению с кинетич. энергией их хаотич. (теплового) движения. Ур-ние состояния для п молей идеального Г., занимающего объем V при т-ре Т и давлении р, имеет вид: pV = nRT, где R = 8,31 ДжДмоль-К)-газовая постоянная (см. Клапейрона - Менделеева уравнение ). Внутр. энергия 1 моля одноатомного идеального газа ? = ³/₂/?Т Дл_Я идеального Г. строго выполняются Бойля-Мариотта закон и Гей-Люссака законы , для реальных Г. эти законы выполняются приближенно-тем лучше, чем дальше р и Т от критич. значений.

Статистич. физика позволяет вычислить макроскопич. св-ва идеального Г., рассматривая его как систему из N квазинезависимых молекул и определяя вероятность раз л. состояний отдельной молекулы. В идеальном Г. для каждой из молекул все окружающие частицы представляют термостат, с к-рым она обменивается энергией. В соответствии с канонич. распределением Гиббса среднее число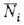 молекул в 1-том состоянии с энергией Е, равно:

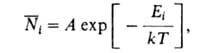
где k- постоянная Больцмана; Л-коэф., зависящий от Т. Применение данной ф-лы в случае, когда движение молекул идеального Г. подчиняется законам классич. механики, позволяет установить распределение молекул по скоростям, а также их пространств. распределение в поле внеш. сил. В соответствии с распределением Максвелла среднее число dN молекул с массой ш, компоненты скоростей к-рых лежат в интервалах от v_x до v_x + dv_x, от v_y до v_y + dv_y и от v. до v_z + dv_z, равно:

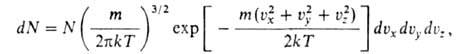
где N- общее число молекул. В любом реальном Г. распределение по скоростям центров инерции молекул представляет собой распределение Максвелла. При наличии внеш. силового поля, в к-ром потенциальная энергия молекулы идеального Г. зависит от координат ее центра инерции, концентрация молекул устанавливается распределением Больцмана:

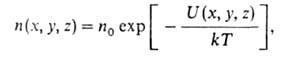
где п₀- концентрация молекул в отсутствие поля; U(x, у, z)- потенциальная энергия молекулы во внеш. поле. В частности, в однородном поле тяжести, направленном вдоль оси z, U = mgz, где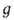-ускорение своб. падения, и распределение плотности газа определяется т. наз. барометрической формулой:

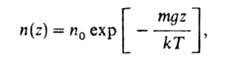
где и₀ - плотность газа в точке z = 0.

При низких т-рах классич. статистика неприменима к идеальному Г. и заменяется квантовой статистикой Бозе-Эйнштейна или Ферми-Дирака для частиц с целым или полуцелым спином соответственно. Т-ра, ниже к-рой отчетливо проявляются квантовые св-ва идеального Г., тем выше, чем меньше масса частиц и чем больше плотность числа частиц. Для обычных Г. соответствующая т-ра очень низка; квантовые эффекты практически существенны лишь для Не, Н₂ и в нек-рой степени для Ne. Квантовую природу системы, проявляющуюся в дискретности энергетич. спектра, необходимо учитывать при описании внутр. состояний молекул (электронных, колебательных, а при низких т-pax-и вращательных). Энергетич. спектр молекул Г., соответствующий их постулат, движению, можно считать квазинепрерывным, т.к. расстояния между соседними уровнями энергии малы.

Применение законов классич. статистики с учетом квантовых закономерностей позволяет рассчитать по молекулярным данным термодинамич. функции Г. (энтропию, внутр. энергию, энергии Гельмгольца и Гиббса), константы хим. равновесия газофазных р-ций, теплоемкость и кинетич. характеристики, знание к-рых требуется при проектировании мн. технол. процессов. Так, теплоемкость идеального Г. может быть рассчитана в классич. теории, если известно число i степеней свободы молекулы. Вклад каждой из вра-щат. и постулат, степеней свободы молекулы в молярную теплоемкость Су равен R/2, а каждой из колебат. степеней свободы-JR (т. наз. закон равнораспределения). Частица одноатомного Г. обладает тремя постулат, степенями свободы, соотв. его теплоемкость составляет ЗЯ/2, что хорошо совпадает с эксперим. данными. Молекула двухатомного Г. обладает тремя поступательными, двумя вращательными и одной колебат. степенями свободы, и, согласно закону равнораспределения, Су = 1R/2, однако это значение не совпадает с опытными данными даже при обычных т-рах. Наблюдаемое расхождение, а также температурная зависимость теплоемкости Г. объясняются квантовой теорией (подробнее см. в ст. Теплоемкость ).

Кинетич. св-ва Г.-теплопроводность, взаимная диффузия (для газовых смесей), вязкость-определяются столкновениями молекул. В простейшем случае явления переноса рассматриваются для разреженного Г., молекулы к-рого считаются упругими шарами, взаимодействующими лишь в момент соударения. В первом приближении все коэф. переноса выражаются через среднюю длину своб. пробега молекулы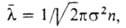 где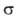-диаметр молекулы. 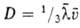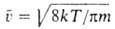Так, , где-средняя скорость теплового движения молекул. Более строгая теория учитывает взаимод. молекул на расстоянии, что приводит к появлению в выражениях для коэф. переноса т. наз. интегралов столкновений, к-рые м. б. рассчитаны, если известен вид потенциала межмолекулярных взаимодействий .

Свойства реальных газов. Неидеальность Г. в молекулярно-кинетич. теории рассматривается как результат взаимод. молекул. В первом приближении ограничиваются рассмотрением парных взаимодействий, во втором-тройных и т.д. Такой подход приводит к вириальному уравнению состояния, коэф. к-рого м. б. теоретически рассчитаны, если известен потенциал межмол. взаимодействий. Наиб. полезно вириальное ур-ние при рассмотрении св-в Г. малой и умеренной плотности. Предложено много эмпирич. и полуэмпирич. ур-ний, связывающих р, V и Т, к-рые либо исходят из нек-рой простой модели взаимодействий (напр., Ван-дер-Ваальса уравнение), либо выражают чисто эмпирич. зависимость, справедливую для определенного класса в-в (см. Уравнения состояния ).

Наличие межмол. взаимодействий оказывает влияние на все св-ва реальных Г., в т.ч. приводит и к тому, что их внутр. энергия зависит от плотности. С этим св-вом связан эффект Джоуля-Томпсона: изменение т-ры газа при его адиабатич. расширении, напр. при протекании с малой постоянной скоростью через пористую перегородку (этот процесс наз. дросселированием). Учет межмол. взаимодействий и внутр. строения молекул необходим при решении мн. теоретич. задач физ.химии. Молекул, к-рые можно было бы принимать как упругие шары, практически не бывает, и при расчете св-в реальных Г. применяют др. молекулярные модели. Из них Наиб. употребительны простые модели гармонич. 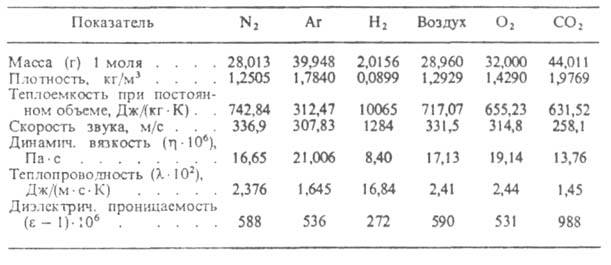осциллятора и жесткого ротатора. Физ. св-ва нек-рых газов приведены в табл. 2 [по данным Автоматизированной информац. системы достоверных данных о теплофиз. св-вах газов и жидкостей (АИСТ)].

Лит.: Гиршфельдер Дж., КертиссЧ., Берд Р., Молекулярная теория газов и жидкостей, пер. с англ., М., 1961; Рид Р., ПраусницДж., Шервуд Т., Свойства газов и жидкостей, пер. с англ., Л., 1982; Смирнова Н. А., Методы статистической термодинамики в физической химии, 2 изд., М, 1982. М. А. Анисимов.

Табл. 2.-ФИЗИЧЕСКИЕ СВОЙСТВА НЕКОТОРЫХ ГАЗОВ ПРИ НОРМАЛЬНЫХ УСЛОВИЯХ (Г= 273,15 К, р = 1,01 * 10⁵ Па)