Химическая энциклопедия

КООРДИНАЦИОННЫЕ ПОЛИЭДРЫ , молекулярные многогранники, вершинами к-рых служат все атомы молекулы (лиганды), непосредственно связанные с произвольно выбранным центр, атомом, а также неподеленные электронные пары, если они имеются. Число вершин равно координац. числу центр. атома. Ребра К. п.-отрезки прямых, попарно соединяющих атомы его координац. сферы. Число топологически разл. полиэдров при заданном числе вершин определяется теорией многогранников. Все реальные К. п. выпуклые. Полиэдрич. молекулы без центр, атома (кластеры металлов, полиэдраны и др.) не относятся к К. п. наиб. распространены К. п. с низшими координац. числами. Числу 4 соответствует тетраэдр [типичен для соед. С, Si, Pt° и др.] и вырожденный случай тетраэдра - плоский квадрат [Pt и др.], числу 5-тригональная бипирамида (Р, Rh, Fe) и тетрагональная пирамида (Mo, W), числу 6-три фигуры: октаэдр [Со³⁺ , Pt⁴⁺ и др.] и реже тригональная призма, пентагональная призма. Более сложные фигуры, напр. тетрагональная антипризма [(CH₃)₈W, координац. число 8], встречаются редко. Перечисл. фигуры наивысшей симметрии среди топологически эквивалентных реализуются в том случае, если лиганды одинаковы или близки по структуре: в большинстве реальных молекул наблюдаются отклонения от правильных К. п. (при сохранении числа вершин, ребер и граней), напр. тригональная пирамида вместо тетраэдра, тетрагональная бипирамида вместо октаэдра. Высокие координац. числа, вплоть до 12, характерны для РЗЭ. Полиэдры, имеющие координац. числа 5 и выше, относятся к стереохимически нежестким молекулам, т.к. склонны к быстрой внутримол. изомеризации без разрыва связей (см. Политопные перегруппировки). 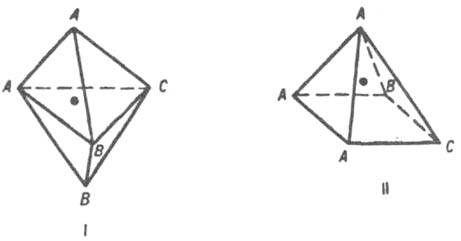Все распространенные К. п. при наличии одинаковых лигандов ахиральны. Хиральность возникает при введении неск. видов лигандов и расположении их в К. п. определенным образом. Плоский квадрат всегда ахирален, т.к. имеет плоскость симметрии; тетраэдр хирален, только если все 4 лиганда различны. В тригональной бипирамиде (ф-ла I) и тетрагональной пирамиде (II) для достижения хиральности достаточно только трех видов лигандов, если они размешены, как показано ниже (жирной точкой обозначен центр. атом):

Представление о К. п. относится как к изолир. молекулам, так и к молекулам в-ва в любом агрегатном состоянии. В бесконечных кристаллич. структурах К. п. укладываются разл. образом в более сложные комбинации. Понятие К. п. применяется при анализе структур молекул, кристаллич. структур, спектроскопических и др. физ.-хим. св-в, а также реакц. способности. Лит.: Гиллеспи Р., Геометрия молекул, пер. с англ., М., 1975; Соколов В. И., Введение в теоретическую стереохимию, М., 1979; Киперт Д., Неорганическая стереохимия, пер. с англ., М., 1985. В. И. Соколов.