Химическая энциклопедия

МАГНИТНЫЙ МОМЕНТ , векторная величина, характеризующая магн. св-ва в-ва. М.м. обладают все элементарные частицы и образованные из них системы (атомные ядра, атомы, молекулы). М.м. атомов, молекул и др. многоэлектронных систем складывается из орбитальных М.м. электронов, спиновых М.м. электронов и ядер и вращат. М.м., обусловленного вращением молекулы как целого. Орбитальный М.м. электрона
,
где е и m_е - абс. значения заряда и массы электрона соотв., с - скорость света, g_e - коэф. пропорциональности, наз. гиромагнитным отношением, вектор L - орбитальный момент кол-ва движения, квадрат к-рого равен 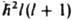(l - орбитальное квантовое число, 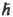- постоянная Планка). Знак минус обусловлен отрицат. зарядом электрона и означает, что направления М.м. m_L и орбитального момента L противоположны. Электронный орбитальный М. м. значителен у многоэлектронных атомов и ионов с частично заполненными d- и f-орбиталями, напр. у атомов и ионов переходных металлов, а также у двухатомных молекул (напр., NO). У многоатомных орг. молекул и радикалов в осн. состоянии электронный орбитальный М.м. практически отсутствует. М.м., обусловленный спином электрона, m_s = — gg_es, где вектор s - собств. момент кол-ва движения (спин), квадрат к-рого равен 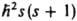(s - спиновое квантовое число), g -множитель Ланде (g-фактор), равный для электрона 2,0023. Направление спинового М.м. электрона также противоположно направлению спина (собств. момента кол-ва движения). М.м. электрона часто выражают через магнетон Бора 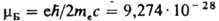Дж/Гс; тогда 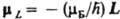и М.м., 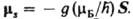обусловленный спином ядра, определяется как m_n = g_nI, где g_n - гиромагнитное отношение для ядра, а квадрат вектора I равен 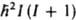, где I - спиновое квантовое число ядра. Ядерный М.м. 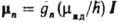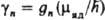часто выражают через ядерный магнетон Дж/Гс, где т_р - масса протона; тогда и , где g_n — g-фактор ядра. Последняя величина имеет разл. значения для разных ядер и определяется внутр. (нуклонной) структурой ядра. Направление М.м. протона совпадает с направлением его спина; для др. ядер (напр., ¹⁵N) оно м. б. противоположным. Орбитальный М.м. m_L, спиновые электронный и ядерный М. м. m_s и m_n пропорциональны соответствующим моментам кол-ва движения L, S и I, но коэф. пропорциональности для них различны. По этой причине направление М.м. атомных и мол. систем, как правило, не совпадает с направлением вектора их полного момента кол-ва движения. У атомов и ионов, содержащих неспаренные электроны, главный вклад в М. м. вносят m_L и m_s: у орг. радикалов М. м. определяется почти исключительно m_s, а небольшой вклад m_L приводит лишь к малому отличию g-фактора радикалов от g-фактора своб. электронов. В магн. поле напряженности Н (вектор с компонентами Н_х, Н_y и Н_z) энергия Е частицы изменяется:

E=E₀ - mH - ¹/₂H.cH,

где E₀ - энергия частицы в отсутствие поля, c - тензор, наз. магн. восприимчивостью частицы (приведены только первый и второй члены разложения в ряд по Н) (см. Зеемана эффект ). Выражение для энергии Е частицы в магн. поле позволяет определить М. м. частицы как производную:

m= - дЕ/дН,

а компоненты тензора магн. восприимчивости c - как втoрые производные:

c_ij = - д²E/дH_iдH_j (i, j = х, у или z).

Для макроскопич. тел М.м. всех составляющих тело частиц усредняются, что приводит к появлению вектора намагниченности М, или М.м. единицы объема. Как правило, для элементарного объема dV

M = M₀ + cH,

где М₀ - намагниченность в отсутствие поля, c - макроскопич. магнитная восприимчивость , к-рая появляется в результате усреднения магн. восприимчивостей c отдельных частиц. У ферромагнетиков и ферримагнетиков M₀ № 0, у диамагнетиков и парамагнетиков M₀ = 0; в магн. поле диамагнетики и парамагнетики намагничиваются (М № 0), причем для диамагнетиков c < 0, для парамагнетиков c > 0. Эксперим. измерение намагниченности М позволяет судить о том, в каких квантовых состояниях находятся составляющие тело частицы (атомы, ионы, молекулы). Однако из-за обменного взаимодействия М.м. изолированных частиц часто не равны М.м. тех же частиц в кристаллич. решетке, вычисляемым по намагниченности чистого в-ва или твердого р-ра. Лит.: Вонсовский С. В., Магнетизм микрочастиц, М., 1973; Калинников В. Т., Ракитин Ю. В., Введение в магнетохимию, М., 1980; Уайт Р., Квантовая теория магнетизма, пер. с англ., 2 изд., М., 1985.