Химическая энциклопедия

МЕТРОЛОГИЯ ХИМИЧЕСКОГО АНАЛИЗА (от греч. metron-мера и logos-слово, учение), учение о мат. обработке результатов хим. анализа. Осн. особенность аналит. определений состоит в том, что их результат зависит от общего хим. состава и физ. св-в анализируемого объекта (т.наз. матричный эффект). Поэтому, напр., методику определения Сu в стали нельзя использовать для определения Сu в руде. Кроме того, анализ, как правило, многостадийный процесс. Сначала обычно отбирают пробу, часто эту пробу разлагают (вскрывают), затем иногда следует разделение компонентов, концентрирование и др. операции. Заключит стадия анализа включает измерения аналит. сигнала-физ. величины (напр., интенсивности спектр. линий, силы электрич. тока), с к-рой корреляционно связано содержание определяемого компонента, и расчет - переход от значения сигнала к содержанию. Каждая из стадий характеризуется своей погрешностью, к-рая входит в общую погрешность анализа.

Аналит. определения редко бывают прямыми; чаще искомое значение содержания находят косвенно по его зависимости от двух или большего числа величин, найденных прямыми измерениями. Связь между аналит. сигналами и содержанием компонентов наз. градуировочной характеристикой, к-рая м. б. представлена в виде ф-л (градуировочная ф-ция), графиков или таблиц. Значение первой производной градуировочной ф-ции при данном содержании определяемого компонента наз. коэф. ч у в с т в и т е л ь н о с т и S, или чувствительностью.

Метрологич. характеристики анализа-погрешность (при условно принятой доверит. вероятности), воспроизводимость, правильность, ниж. граница определяемых содержаний и предел обнаружения - имеют смысл только для данной методики, в к-рой подробно описаны все операции и условия анализа. Область содержаний компонента, в к-рой применима данная методика, наз. д и а п а з о н о м о п р е д ел я е м ы х с о д е р ж а н и й.

П о г р е ш н о с т ь отдельного результата анализа: D = = С — а, где С-среднее результатов п параллельных определений, а-истинное содержание или, поскольку оно обычно неизвестно, т.наз. действительное содержание, напр. аттестованное значение содержания определяемого компонента, приведенное в паспорте стандартного образца. Погрешность можно выражать отношением D/a или D/С (в долях от единицы или в процентах).

Воспроизводимость характеризует случайное рассеяние результатов. Иногда в случае рассеяния результатов, полученных по данной методике в максимально близких условиях, напр. при параллельных определениях, когда интервал времени получения результатов соизмерим с длительностью единичного определения, используют термин "сходимость", а для характеристики близости результатов анализа, полученных в разных условиях (разл. исполнители, аппаратура, разные периоды времени и т. д.),-термин "воспроизводимость". Рассеяние результатов анализа, полученных в разных лабораториях, характеризуется межлабораторной воспроизводимостью; накопление таких данных позволяет формировать производств. нормы. Количественно воспроизводимость оценивают стандартным (средним квадратичным) отклонением 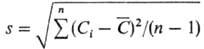или дисперсией V = s². Здесь С_i-результаты отдельных определений, п- число этих результатов, С-среднее арифметическое п результатов. Часто пользуются относит. стандартным отклонением s_r = s/C (в долях единицы); эта же величина в % наз. коэф. вариации u. Значение s и s_r заметно изменяются при изменении С в широком диапазоне. В области определяемых содержаний, близких к их ниж. границе, зависимость s =f(C)удается представить линейным ур-нием s = s₀ + b₁С (где s₀-стандартное отклонение в холостом опыте), в области больших содержаний - ур-нием lgs = = lg A + В lg С или lgs_r = lg A - (1 - B)lg С, где А и В- константы. Для хорошо отработанных методик В часто приближается к 0,5, тогда дисперсия s² = A²C. В узком диапазоне определяемых содержаний можно считать s постоянным. В техн. документации стандартное отклонение нормируют в зависимости от содержания обычно в виде таблиц, разбивая весь диапазон определяемых содержаний на небольшие интервалы.

В случае косвенных аналит. определений С = j (х, у,.... z), где х, у, ..., z- результаты прямых измерений. Если они не зависят друг от друга, за оценку действительного значения содержания принимают 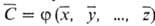, где 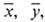..., 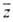-средние арифметич. значения результатов соответствующих прямых измерений. Если разложить нелинейную ф-цию j(х, у, .... z)в ряд Тейлора и ограничиться членами первого порядка, то получится оценка дисперсии результата анализа:

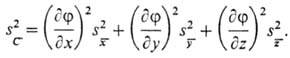
Это т. наз. закон накопления (распространения) погрешностей. В случае зависимых величин при расчете учитывают корреляцию между ними.

Экспериментально найденное стандартное отклонение и знание закона распределения результатов в рассматриваемой совокупности позволяют выражать результат очередного анализа в виде д о в е р и т е л ь н о г о и н т е р в а л а для условно принимаемой доверит. вероятности Р (обычно Р = 0,95), т. е. интервала, в к-ром с данной вероятностью находится истинное значение определяемой величины. Распределение результатов количеств. анализа обычно аппроксимируют законом нормального распределения плотности вероятности. Для того чтобы установить, что распределение результатов не противоречит нормальному закону, рекомендуют разл. статистич. критерии согласия. Дифференциальная форма нормального закона распределения в нормированном и центрированном виде: 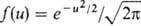, где и = (С — m) , m - мат. ожидание случайной величины С.

Интегральная ф-ция распределения табулирована, что позволяет легко рассчитывать доверит. интервал для заданной доверит. вероятности.

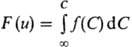
Когда обрабатывают ограниченные по объему выборки из нормальной совокупности, используют спец. t-распределе-ние, в к-ром квантиль 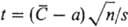, где 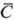-среднее из п параллельных определений, s -оценка стандартного отклонения, найденная из п параллельных определений. Пользуясь табулированным t-распределением, оценивают доверит. интервал, к-рый с доверит. вероятностью Р включает неизвестное действит. содержание 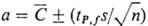, где f-число степеней свободы (f= n — 1). Если для оценки s была использована выборка объема т > n, полученная в таких же условиях, то для нахождения табличного значения t принимают f = m — 1, а в знаменателе приведенного выше выражения остается .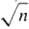

Для сопоставления характеристик воспроизводимости результатов анализа, полученных по разным методикам, пользуются F-распределением: F = s²_{1 2}², где s²₁ и s₂²-дисперсии результатов двух сравниваемых методик (s₁ > s₂). Если найденное из эксперимента значение F превышает табличное F_f1,f2,p, различие сравниваемых дисперсий считают значимым с доверит. вероятностью Р.

Для хим. анализа имеет значение также распределение Пуассона Р_т = m^me^-m !, где P_m-вероятность появления целочисленного значения т, m-мат. ожидание и совпадающая с ним по величине дисперсия. По этому закону распределяются результаты измерений аналит. сигналов в виде целочисленных значений, напр. число импульсов в рентгеноспектральном или радиохим. методе анализа.

Для нек-рых методов и условий анализа, напр. при определении следов, закон распределения результатов может отличаться от нормального и оставаться невыясненным. В этом случае для оценки значения доверит. интервала используют т. наз. непараметрич. статистику. Напр., для неизвестного симметричного закона распределения используют неравенство Чебышева в виде Р{|С_i — а| >= ks} <= <= [2/3k] , где k > 0. Доверит. интервал (bks)для той же вероятности получается более широким, чем в случае нор-мального распределения.

В хим. методах анализа применяется специфич. характеристика случайного рассеяния результатов - расхождение результатов параллельных определений (чаще всего двух) между собой-размах варьирования R_n = C_max — C_min. При нормальном распределении результатов средний размах 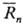= d_n,ms, где d_n,m - табулированный коэф., п- число параллельных определений, между к-рыми наблюдается размах, т-число образцов в выборке; напр., для расхождения двух параллельных определений при т >= 10 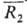= 1,13s. Допустимые расхождения параллельных определений - верх. граница размаха при фиксированной доверит. вероятности Р: R_В,n,Р = w_n,qs, где w_n,q-табулированный коэффициент.

П р а в и л ь н о с т ь характеризует систематич. погрешность-систематич. смещение результатов от действит. значения. Для оценки правильности используют разные способы (анализ образца разл. методами, межлаб. анализ, теоре-тич. расчет и др.). Один из них-анализ стандартных образцов или синтетич. образцов сравнения. При этом, поскольку систематич. погрешности всегда выявляются на фоне случайных, по существу решают вопрос о незначимости расхождения между найденным 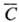и паспортным содержанием а компонента: 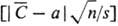< t_P,f, где t_P,f- табличный коэф. Стьюдента для принятой вероятности Р и числа степеней свободы f=т—1, т-число определений, по к-рым найдено s. В этом простейшем способе расчета подразумевается, что погрешностью аттестации или синтеза можно пренебречь. Для заключения о правильности результатов, получаемых по данной методике, т.е. о незначимости суммарной систематич. погрешности, предпочтительнее использовать неск. стандартных образцов в пределах диапазона определяемых содержаний. Стандартные образцы с содержанием определяемого компонента С_со анализируют, строят прямую 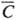= А + ВС_со, где А характеризует постоянную, или аддитивную, составляющую систематич. погрешности, а величина (В— 1)С_со-пропорциональную, или мультипликативную, составляющую; оценивают наличие систематич. погрешности, проверяя значимость неравенств |A|>0, |B— 1|>0с учетом корреляции А и В между собой.

В другом способе (особенно удобном для методик, связанных с растворением пробы) для нахождения А и В используют вариацию аналит. навесок и добавки. Для двух навесок (напр., в соотношении по массе 1:2) можно записать 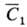= А + BС_ист и 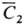= А + 2BС_ист, где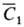и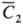-усредненные результаты анализа для двух разных навесок одного образца; С_ист-истинное содержание определяемого компонента в образце. Тогда 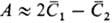. Для оценки В анализируют несколько одинаковых навесок, но в часть из полученных р-ров добавляют определяемый компонент в кол-ве С₀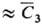. Тогда 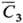= А + BС_ист, С₄ = А + В(С_ист+ С₀), откуда В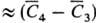,/С₀.

В инструмент. методах анализа твердых проб важный показатель правильности и воспроизводимости - остаточная дисперсия s₀² экспериментально найденного аналит. сигнала относительно градуировочной ф-ции у = F (С), то есть s₀² = S [Y_i - F(C_i)]²/f, где f-число степеней свободы. Во мн. случаях причина рассеяния точек относит. градуировочной линии-неучтенный матричный эффект. При этом наблюдается значимое превышение остаточной дисперсии над дис-

Персией воспроизводимости, что указывает на возможную систематич. погрешность.

Т о ч н о с т ь-качеств. характеристика анализа, отражающая близость результатов к истинным значениям; высокой точности соответствуют малые систематич. и случайные погрешности, т.е. правильность и высокая воспроизводимость.

Н и ж н я я г р а н и ц а о п р е д е л я е м ы х с о д е р ж а н и й С_н может лимитироваться нормированным уровнем относит. стандартного отклонения s_r. При этом исходят из экспериментально установленной зависимости s_r = j (С), по к-рой находят С_н для предельного уровня s_r. Иногда нормируют не s_r, а относит. полуширину доверит. интервала. Напр., если для нормального распределения величина t_P,fs_r/C_н должна быть не более ¹/₃, тогда С_н >= 3t_P,fs_н, где s_н-стандартное отклонение, соответствующее С_н. Для числа степеней свободы f>= 20 и доверит. вероятности Р = 0,95 табличный коэф. t_P,f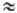2 и, следовательно, С_н >= 6s_н. Оценки s_н и С_н по эксперим. зависимостям достаточно просты только для линейных градуировочных ф-ций. В др. случаях необходим более сложный расчет погрешностей косвенных измерений.

Потенциальные возможности определения по данной методике миним. содержаний компонентов характеризуют п р е д е л о м о б н а р у ж е н и я-наименьшей концентрацией С_мин (относит. предел обнаружения) или наименьшей массой q_мин (абсолютный) компонента, при к-рой его можно обнаружить с заданной доверит. вероятностью. При определении малых (следовых) кол-в всегда приходится учитывать аналит. сигнал для пробы, практически не содержащей искомого компонента (сигнал холостого опыта). Для расчета предела обнаружения важна флуктуация холостого сигнала. По рекомендации ИЮПАК для градуировочной ф-ции y = y_хол + SC аналит. сигнал, соответствующий С_мин, y_мин = у_хол + 3s_хол, тогда С_мин = 3s_хол/S, где y_хол - усредненный аналит. сигнал холостого опыта, s_хол- стандартное отклонение холостого сигнала, 3-условный коэф., к-рый при неизвестном законе распределения сигнала соответствует для холостой пробы вероятности Р{|у —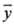_хол| > 3s_хол}<= <=0,1. Ошибочное наблюдение у — у_хол > 3s_хол, когда должно быть y-y_xол = 0, наз. ошибкой 1-го рода. Если критич. уровень у_крит = у_хол + 3s_хол, то весьма высокой будет вероятность ошибки 2-го рода, т.е. ошибочного наблюдения y - y_xол < Зs_хол для фактического у — у_xoл >= 3s_хол. Напр., для С>=C_мин эта вероятность составит 0,5, т. е. в 50% из большого числа испытаний будет сделано ошибочное заключение об отсутствии компонента.

Для улучшения метрологич. характеристик методик предпринимают статистич. дисперсионный анализ с целью выявления "слабого звена". Предполагают, что каждое звено (этап анализа) вносит свою долю в общую погрешность анализа. Допуская независимость и аддитивность частных дисперсий, обусловленных каждым из звеньев, можно, оценив их спец. приемами, записать s²_S = s²₁ + s²₂ + ... + s²_i и усовершенствовать лишь 1-2 звена, в к-рых дисперсии наибольшие.

Автоматизация анализа и широкое использование ЭВМ позволяют улучшить метрологич. характеристики хим. анализа, т.к. повышается единообразие дозировок, смешения, титрования, фотометрирования и т. п., что приводит к снижению случайных погрешностей анализа. Кроме того, автоматизация обычно повышает скорость выполнения определений и может привести к уменьшению их доверит. интервалов, позволяя увеличить число параллельных определений, выполняемых за фиксир. промежуток времени. При использовании нек-рых методов мат. моделирования с применением ЭВМ можно получать более правильную градуи-ровочную характеристику, в значит. мере учесть матричный эффект. Расчеты на ЭВМ позволяют во многих физ.-хим. и физ. методах анализа восстанавливать действит. форму контуров аналит. сигналов и обеспечить более высокое их разрешение, в результате чего повысить точность, снизить предел обнаружения. ЭВМ существенно сокращают затраты труда на обработку результатов анализа, повышают их надежность.

Лит.: Бурдун Г. Д., Марков Б. Н., Основы метрологии, 2 изд., М., 1975; Метрологическое обеспечение производства, под ред. А. А. Тупиченкова, М., 1982; Шаевич А. Б., Аналитическая служба как система, М., 1981; Ко-марь Н. П., Химическая метрология. Гомогенные ионные равновесия, Харьков, 1983; ЧарыковА.К., Математическая обработка результатов химического анализа, Л., 1984. Е.Л. Гринзайд.