Химическая энциклопедия

МОЛЕКУЛЯРНЫЕ ИНТЕГРАЛЫ в квантовой химии, название интегральных выражений (интегралов), к-рые используются для записи в матричной форме электронного ур-ния Шрёдингера [Шредингера], определяющего электронные волновые ф-ции многоэлектронной молекулы (мол. системы). Подынтегральными ф-циями в М. и. являются атомные или мол. орбитали (волновые ф-ции) отдельных электронов либо орбитали, преобразованные теми операторами, к-рые входят в оператор Гамильтона и соответствуют определенным физ. величинам (напр., потенциалу взаимод. электронов, дипольному моменту и др.). Интегрирование производят по всему объему, в к-ром вероятность обнаружения каждого электрона, определяемая интегралом по этому объему от произведения его волновой ф-ции j на комплексно-сопряженную величину j*, равна 1. М. и. обычно имеют следующий вид:

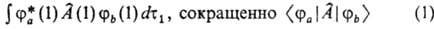
(т. наз. о д н о э л е к т р о н н ы е и н т е г р а л ы) либо

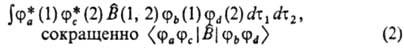
(т. наз. д в у х э л е к т р о н н ы е и н т е г р а л ы). В этих выражениях j_a(1), j_b(1), j_с(2) и j_d (2) - атомные или мол. орбитали, зависящие от переменных первого (1) или второго (2) электрона, dt₁ и dt₂-элементы объема для этих электронов, 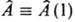- одноэлектронный, а 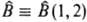- двухэлектронный операторы, к-рые зависят от переменных соотв. одного или двух электронов и действуют на волновые ф-ции j_b(1) и j_b(1)j_d(2) (см. Квантовая механика ).

Классификация одно- и двухэлектронных М. и. связана с видом подынтегральных ф-ций и операторов. Так, в простейшем случае, когда 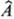-единичный оператор (умножение на единицу), т.е., по существу, в интеграле (1) оператор отсутствует, получающийся одноэлектронный М. и. называют и н т е г р а л о м п е р е к р ы в а н и я орбиталей j_а(1) и j_b(1). По значению интегралов перекрывания атомных орбиталей часто судят о прочности хим. связи между атомами А и В, если j_a(1) и j_b(1)- атомные орбитали, соответствующие этим атомам. Если 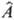= — Z_ce²/R_1c-oпepaтор потенциальной энергии взаимод. электрона 1 и ядра С, заряд к-рого Z_c (R_1c-расстояние между электроном 1 и ядром С), соответствующий М. и. называют интегралом электрон-я д е р н о г о в з а и м о д е й с т в и я. К числу одноэлектронных М. и. относят также интегралы кинетич. энергии, интегралы дипольного момента и др.

В выражениях для двухэлектронных М. и. наиб. часто встречается оператор кулоновского отталкивания электронов 1 и 2, т.е. 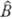(1, 2) = е²/r₁₂, где r₁₂-расстояние между электронами. При этом М. и. вида

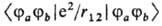
наз. кулоновскими. Они соответствуют классич. элект-ростатич. взаимодействию двух зарядов, один из к-рых распределен в пространстве с плотностью r_а(1) = j*_a(1) х х j_a(1), а другой-с плотностью r_b (2) = j_b* (2) j_b (2). Если переставить индексы а и b у ф-ций, следующих за символом оператора e²/r₁₂, получаются М. и. вида

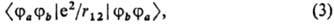
к-рые наз. о б м е н н ы м и. Появление обменных М. и. в выражениях для энергии и для др. св-в многоэлектронных мол. систем связано с принципом Паули и не имеет аналогии в классич. теории (см. Обменное взаимодействие ).

М. и. различают также по локализации орбиталей j_а, j_b,... Если эти орбитали локализованы у одного из атомных ядер молекулы (или в области между ядрами), т.е. если они относятся к одному центру (ядру или к.-л. точке в пространстве между ядрами), то М. и. наз. одноцентровыми; если j_a относится к центру А, а j_b-к центру В, говорят о д в у х ц е н т р о в ы х М. и., и т.д. При этом в число центров включаются и те, от переменных к-рых зависят также операторы А(1)или В(1,2); так, если A(1)-упомянутый выше оператор потенциальной энергии взаимод. электрона 1 с ядром С, то это ядро также считается центром для М. и.

Нек-рые М. и. с одинаковыми названиями имеют разл. смысл в разных квантовохим. методах. Так, в методе Хюкке-ля резонансными М. и. наз. ненулевые недиагональные матричные элементы эффективного одноэлектронного гамильтониана (см. Молекулярных орбиталей методы ), а в полуэмпирических методах типа методов полного пренебрежения дифференц. перекрыванием резонансные М. и.-лишь такие слагаемые недиагональных матричных элементов фо-киана, к-рые при конкретных расчетах заменяются на те или иные комбинации эмпирич. параметров. В валентных связей методе обменными М. и. наз. матричные элементы 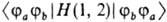двухэлектронного гамильтониана H(1, 2) в базисе атомных орбиталей, что отличается от выражения (3) для обменных М. и. в методах мол. орбиталей.

Расчет М. и. всегда представлял собой одну из важнейших вычислит. проблем квантовой химии, к-рая стала особенно острой в связи с развитием и широким применением неэмпирических методов . Для упрощения вычислений проводят поиск оптимальных базисных ф-ций, к-рые позволяют получать наиб. простые ф-лы для расчета М. и. В частности, для многоатомных молекул оптимальными базисными ф-циями оказались орбитали гауссова типа (см. Орбиталъ ). Еще более трудная проблема - рост числа М. и. с увеличением кол-ва базисных орбиталей: если число последних - М, то число М. и. превышает М⁴/8. При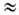 М 10² приходится рассчитывать 10⁷-10⁸ М. и. Поскольку обычно мол. системы рассматривают в адиабатическом приближении , требующем вычислений в отдельности для каждой фиксированной геом. конфигурации ядер, а число таких конфигураций для многоатомных молекул достаточно велико даже при описании локальных участков поверхности потенциальной энергии , то становится ясным, какие трудности связаны с расчетами М. и. или пересчетом на каждом шаге итераций. Именно из-за этих трудностей активно разрабатывают полуэмпирич. методы, основанные, напр., на полном или частичном пренебрежении дифференц. перекрыванием. В подобных методах число М. и. увеличивается с ростом числа М базисных ф-ций не быстрее, чем М². В полуэмпирич. методах используют модельные представления, согласно к-рым отдельные М. и: либо нек-рые их комбинации рассматривают как параметры, имеющие определенный физ. смысл. Подобный подход позволяет наглядно интерпретировать расчетные результаты и сопоставлять их для разных мол. систем.

Лит. см. при ст. Квантовая химия . Н. Ф. Степанов.