Химическая энциклопедия

МОЛЕКУЛЯРНЫХ ПУЧКOВ МЕТОД , используется для изучения взаимодействий атомов и молекул в условиях их однократных (единичных) столкновений (упругих, неупругих и сопровождающихся хим. р-цией), а также для исследования св-в изолир. атомов и молекул, взаимод. газовых потоков с пов-стью твердого тела, эпитаксиального наращивания тонких пленок и т.п. Основан на создании м о л е к у л я р н ы х п у ч к о в-направленных потоков атомов, молекул, радикалов, др. нейтральных частиц, движущихся в высоком вакууме практически без взаимод. между собой. Мол. пучки характеризуются распределением частиц по скоростям и внутр. степеням свободы, интенсивностью (числом частиц, прошедших через телесный угол за секунду), средней скоростью частиц и их кинетич. т-рами. Св-ва мол. пучков зависят от методов их получения.

Источники. Наиб. применение имеют мол. пучки, получаемые в эффузионных и газодинамич. источниках. В э ф ф у з и-о н н о м и с т о ч н и к е пучок формируется при помощи диафрагм, вырезающих часть потока газа, истекающего из камеры в вакуум через небольшое отверстие. Диаметр отверстия D и давление в камере подбирают таким образом, чтобы выполнялось условие: число Кнудсена Кn = l/D >> 1, где l-средняя длина своб. пробега частиц в источнике. При этом имеет место мол. истечение газа (эффузия), а не газодинамич. поток. Распределение частиц в пучке по скоростям является максвелловским и соответствует т-ре источника. Вследствие этого поступат. энергия частиц не превышает ~0,5 эВ. Т. наз. многоканальные формирователи пучков позволяют значительно повысить интенсивность пучка при таком же расходе газа. В эффузионных источниках обычно получают пучки активных частиц: атомов водорода, хлора, фтора, разл. металлов.

Г а з о д и н а м и ч е с к и е и с т о ч н и к и основаны на использовании своб. расширения струи при истечении газа в вакуум; при этом выполняется условие Кn << 1. Мол. пучок формируется посредством вырезания ядра струи скиммером- конусообразной диафрагмой с острыми кромками. Полная энтальпия газа в источнике преобразуется в кинетич. энергию направленного движения частиц со средней скоростью и и кинетич. энергию хаотич. движения частиц в системе координат, движущейся со скоростью и. Степень преобразования энтальпии в кинетич. энергию направленного движения обычно определяется числом Маха Ма = (2/g)^1/2и/a, где a-наиб. вероятная случайная скорость частиц в системе координат, движущейся со скоростью u, g = C_p/C_u-отношение уд. теплоемкостей газа при постоянном давлении и объеме соответственно. При ускорении газа максвелловское распределение частиц по скоростям нарушается, ф-ция распределения сужается, т. е. энергия частиц соответствует более низким кинетич. т-рам; кроме того, молекулы в таком пучке "охлаждены" и по внутр. степеням свободы. В случае получения мол. пучка из смеси газов можно добиться того, чтобы при определенных условиях в источнике все молекулы независимо от их мол. массы имели близкие средние скорости, т. е. чтобы кинетич. энергия молекул в пучке была пропорциональна их мол. массам. Обычно с целью получения высокой кинетич. энергии (до неск. десятков эВ) в легкий газ-носитель, обычно гелий, добавляют 1-5% более тяжелых частиц.

Эксперименты со скрещенными пучками дают наиб. полную информацию о взаимод. между частицами, в т. ч. о хим. р-циях, позволяя проследить траектории рассеянных частиц или продуктов р-ции. Этого достигают тем, что сначала определяют скорости, углы взаимод. и др. исходные состояния пучков реагентов, а затем измеряют распределение рассеянных частиц, в т.ч. продуктов, по скоростям, внутр. степеням свободы, углам рассеяния. Установка со скрещенными пучками состоит из неск. вакуумных камер с диффе-ренц. откачкой, источников мол. пучков (один из к-рых, как правило, газодинамический), мех. модуляторов пучков, детектора, разл. селекторов для выделения частиц с энергиями в заданном интервале значений, систем управления экспериментом, сбора и обработки данных. Распределения рассеянных частиц по скоростям обычно определяют времяпролет-ным методом, при к-ром измеряют времена прохождения частицами известного расстояния. Применяют разл. детекторы: масс-спектрометры с ионизацией электронным ударом или лазерным излучением; с поверхностной ионизацией; манометрич.; микровесы; полупроводниковые; лазерные (основанные на лазерно-индуцир. флуоресценции).

В общем случае для процесса типа A_i + B_jC_k + D_l, где индексы i, j и k, l характеризуют соотв. квантовые состояния реагентов и продуктов взаимод., в идеальном эксперименте можно определять непосредственно детальное дифференц. сечение взаимодействия s_kl/ij (см. Бимолекулярные реакции , Столкновений теория ). Оно пропорционально измеряемому потоку частиц продуктов C_k или D_l в заданном направлении и зависит от кинетич. энергии взаимод. и начальных квантовых состояний частиц реагентов А_i и В_j. Однако экспериментально измеряемые величины всегда усреднены по условиям, отличающим реальный эксперимент от идеализир. схемы. К таким условиям относят: распределение частиц в пучках по скоростям и внутр. степеням свободы, неоднородность пучков по сечению, телесный угол, стягиваемый детектором, и т. п. Поэтому для определения сечений хим. р-ций, упругих или неупругих взаимод. используют мат. модели, связывающие реальные начальные условия с экспериментально определяемыми величинами. При анализе результатов экспериментов по рассеянию мол. пучков широко применяют кинематич. диаграммы, отражающие связь скоростей частиц реагентов и продуктов с динамикой протекающих процессов.

Измерения распределения частиц-продуктов по скоростям и углам рассеяния позволили установить существование разл. типов р-ций. Для нек-рых р-ций угловые распределения продуктов оказались асимметричными в координатах центра масс, т.е. частицы продуктов разлетаются преим. в определенном направлении. Это означает, что время протекания таких р-ций порядка длительности столкновений 10^-13-10^-15 с. Их наз. п р я м ы м и р е а к ц и я м и, т.к. при этом не происходит образования комплекса сталкивающихся частиц. Различают прямые р-ции срыва (срывные р-ции) и прямые р-ции рикошета (рикошетные р-ции). Для р е а к ц и й срыва характерны большие сечения и рассеяние продуктов в переднюю полусферу области взаимод., как показано на рис. а. Кинетич. энергия продуктов не превышает кинетич. энергии реагентов, причем осн. часть выделяемой при р-ции энергии расходуется на возбуждение внутр. степеней свободы частиц продуктов - сильное колебат. и сравнительно слабое вращат. возбуждение. Типичным примером срыва служит р-ция К + I₂ KI + I, на рис. а показана контурная диаграмма эксперим. распределений молекул KI относительно угла рассеяния 6 (угол между направлением разлета и направлением вектора скорости сталкивающихся частиц); видно преим. рассеяние продуктов р-ции вперед по отношению к направлению вектора скорости атома К.

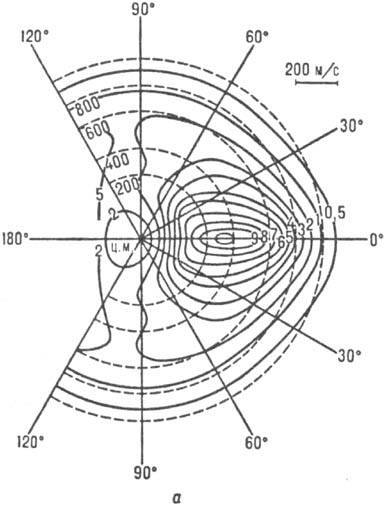
Контурные диаграммы интенсивности углового распределения продуктов для р-ций К + I₂KI + I (а), К + CH₃IKI + СН₃ (б) и Hg + I₂ HgI + I (в) в системе координат центра масс (ц. м.). Указаны углы рассеяния (град) и скорости сталкивающихся частиц (м/с). Контурные линии изображают детальное дифференц. сечение р-ций.

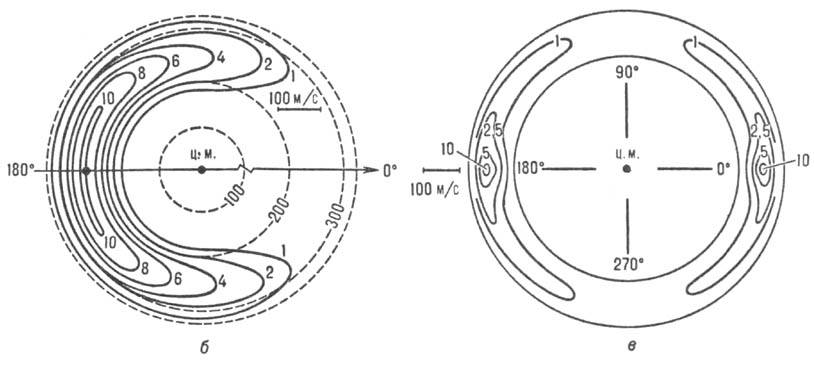
В р е а к ц и я х р и к о ш е т а (напр., К + CH₃I KI + СН₃) продукт KI "рикошетирует", как если бы сталкивающиеся частицы были твердыми шарами. При этом угловое распределение продукта ограничивается преим. задней полусферой (рис. б)и практически вся энергия взаимод. реализуется в виде поступат. энергии продуктов.

Контурные карты интенсивности рассеяния продуктов для нек-рых атомно-мол. р-ций обладают симметрией относительно направления, отвечающего углу q = 90°. Наличие этой симметрии указывает на образование промежут. комплекса сталкивающихся частиц. В случае р-ций, идущих через образование долгоживущего комплекса, распределение продуктов характеризуется наличием двух максимумов. Так, при р-ции Hg + I₂ HgI + I продукты рассеиваются "вперед" и "назад" (рис. в). Возможно также образование короткоживущего промежут. комплекса, время жизни к-рого определяется одним или неск. колебаниями.

Сопоставление теоретически предсказанных и эксперим. распределений по углам рассеяния, скоростям и внутр. степеням свободы частиц-продуктов позволяет проводить проверку данных, полученных расчетным путем, напр. на основе активированного комплекса теории .

Метод молекулярных пучков в сочетании с лазерно-индуци-рованной флуоресценцией широко используется в изучении однофотонной и многофотонной диссоциации и ионизации молекул (см. Многофотонные процессы ). Эффективно также применение лазеров для оптич. накачки реагентов в высшие энергетич. состояния при изучении динамики элементарного акта хим. р-ций, т.к. оказывается возможным установить зависимость скорости р-ции от энергетич. состояния реагентов. Это является ценным дополнением к результатам, полученным из измерений зависимости сечения р-ции от скорости сталкивающихся реагентов.

Рассеяние молекулярных пучков поверхностью твердого тела позволяет получать детальную информацию о св-вах морфологии и степени разупорядочения пов-сти. При неупругом рассеянии изучается обмен энергий между посту-пат., вращат. и колебат. степенями свободы частиц в пучке и колебат. степенями свободы частиц на пов-сти, процессы адсорбции и десорбции. С помощью мол. пучков исследуются хим. р-ции, в к-рых пов-сть действует как катализатор в процессах диссоциации или рекомбинации (напр., диссоциация Н₂ на пов-сти вольфрама) или является одним из реагентов (напр., окисление пов-сти графита).

Мол. пучки из газодинамич. источников обычно содержат кластеры-от димеров до содержащих неск. сотен атомов. Лазерное распыление твердых мишеней в сопле газодинамич. источника позволило получить кластерные пучки практически всех элементов периодической системы, в т. ч. получить такие стабильные молекулы, как С₆₀. Эксперименты с кластерными пучками проводятся для исследования межатомных сил, физ.-хим. св-в кластеров и их зависимости от размера кластера, а также для получения тонких пленок (см. Эпитаксия ), каталитич. пов-стей и модификации пов-сти с целью придания ей заданных св-в.

Начало использования мол. пучков для изучения хим. р-ций положено работами Е. Тейлора и Ш. Датца (1955). Важнейший вклад в изучение динамики элементарного акта хим. превращения сделан Д. Хершбахом (Нобелевская премия 1986, совместно с Ли Яном и Дж. Полани).

Лит.: Хершбах Д. Р., Молекулярная динамика элементарных химических реакций, пер. с англ., М., 1988; Ли Ю. Ц., Исследования элементарных химических процессов в молекулярных пучках, пер. с англ., М., 1988; Bernstein R. В., Chemical dynamics via molecular beam and laser techniques, Oxf.-N. Y., 1982.

Д. Н. Трубников.