Химическая энциклопедия

МОНОМОЛЕКУЛЯРНЫЕ РЕАКЦИИ , элементарные хим. р-ции, в к-рых изменяется состав или строение только одной молекулы, радикала или иона, напр. распад, изомеризация. Часто М.р., особенно распад молекулы (обычно на два фрагмента), являются начальными стадиями сложных процессов - крекинга, деструкции полимеров и др. В газах при повышении т-ры Т или уменьшении плотности хим. равновесие смещается в сторону продуктов распада, вследствие чего значительно возрастают теплоемкость и энтальпия системы. Константы равновесия М. р. необходимы для расчета равновесного состава и термодинамич. ф-ций газов и приводятся в справочниках.

М.р., как правило, эндотермичны, и для р-ции необходима активация - переход частицы А в активное состояние А*, энергия к-рого достаточна для преодоления потенц. барьера на пути р-ции. Активная молекула может самопроизвольно превратиться в продукт либо дезактивироваться. Эти качеств. черты М.р. описываются схемой Лин-демана:

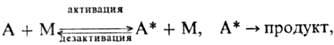
где М-частицы среды (атомы, молекулы, электроны, ионы) или стенка сосуда. Стадия самопроизвольного распада в более детальной схеме (Р.А. Маркус, O.K. Раис) представляется двумя последоват. переходами: 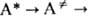продукт, где 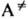-переходное состояние (активир. комплекс), в к-ром энергия, достаточная для р-ции, уже сосредоточена на разрываемой связи (в общем случае-на координате реакции ).

Константа скорости М.р. 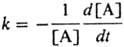, где [А]-концентрация реагирующих молекул, t-время. При заданной т-ре k пропорциональна давлению р в области низких р (обозначается k₀) и не зависит от р в области достаточно высоких р (обозначается 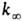). В переходной области давлений k монотонно изменяется от k₀ до 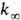. Для молекул, состоящих из 5-10 атомов, при ~ 300-1000 К середина переходной области, определяемая условием k/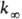 = 1/2, расположена обычно при р ~ 10²-10⁴ Па. С уменьшением числа атомов в молекуле и с повышением Т переходная область смещается в сторону больших р. В рамках схемы Линдемана зависимость k от р объясняется тем, что при низких р лимитирующая стадия р-ции - активация, имеющая второй порядок, а при высоких р-стадия А*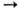продукт, имеющая первый порядок. В двухатомных молекулах имеется всего одна колебат. степень свободы, и колебания всегда соответствуют движению вдоль координаты р-ции. Состояния А* и 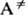двухатомной молекулы тождественны, самопроизвольный распад происходит за время порядка периода колебаний. Это время практически всегда настолько мало, что ниж. граница переходной области давлений соответствует очень большим плотностям, не реализуемым в газах. Поэтому диссоциация двухатомных молекул в газах всегда имеет второй порядок. Для М.р. в конденсир. средах k практически не зависит от р.

Наблюдаемая зависимость 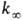от Т приближенно описывается ур-нием Аррениуса с энергией активации 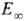, к-рая для распада обычно мало отличается от энергии D разрываемых связей, и предэкспоненц. множителем А, значение к-рого составляет в большинстве случаев 10¹³-10¹⁵ с^-1. Большие значения А могут соответствовать случаям, когда при переходе в молекуле появляются новые вращат. степени свободы. Существ. отклонения 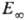от D и аномально малые значения А могут наблюдаться, если р-ция идет по т. наз. н е а д и а б а т и ч е с к о м у к а н а л у (т.е. с изменением электронного состояния молекул). С повышением т-ры адиабатич. канал протекания р-ции (без изменения электронного состояния молекул) дает больший вклад в суммарное значение константы скорости. В той области т-р, где протекание р-ции по обоим каналам дает сопоставимые вклады, константу скорости k выражают в виде суммы двух ур-ний Аррениуса-с двумя значениями энергии активации и предэкспоненц. множителя. Зависимость k₀ от Т выражена слабее, чем .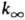

Р-ция, обратная мономолекулярному распаду, является бимолекулярной и имеет третий (при низких р)или второй (при высоких р)порядок. Изомеризация является М. р. как в прямом, так и в обратном направлении.

Существует неск. теоретич. представлений, на основании к-рых возможен приближенный расчет константы скорости М. р. Для адиабатич. р-ций наиб. удовлетворит. результаты дает статистич. т е о р и я Р а и с а-Р а м с п е р г е р а-К а с с е-л я-М а р к у с а (сокращенно РРКМ). В этой теории предполагается, что заселенности всех квантовых состояний молекулы с одинаковой энергией одинаковы независимо от различий в скорости возникновения и гибели каждого состояния. Это позволяет найти ф-цию распределения молекул по энергии f(E), к-рая содержит лишь усредненные константы скорости перехода из состояния с энергией Е в состояние с энергией Е [обозначается k(E, E)] и самопроизвольного распада [обозначается k(E)]. Ф-ция k(E)вычисляется на основе активированного комплекса теории и выражается соотношением:

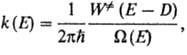
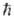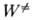где - постоянная Планка, (Е — D) - число состояний активир. комплекса с энергией в интервале значений от нуля до (Е — D), причем учитываются все состояния, кроме относящихся к координате р-ции, W (E)-плотность колебат. и вращат. состояний, т.е. число состояний молекулы, приходящихся на единичный интервал энергии вблизи Е. Ф-ция k(E, E)определяется механизмом передачи энергии при столкновениях. Если вероятность дезактивации при одном столкновении близка к единице (т. наз. с и л ь н ы е с т о л к н ов е н и я), эта ф-ция имеет вид:

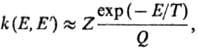
где Q-статистич. сумма, Z- число столкновений в единицу времени (газокинетич. число). Расчет f(E), k, 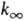и k₀ производят по ф-лам:

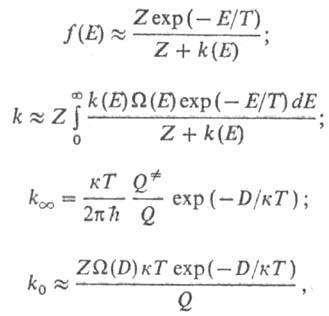
где к -постоянная Больцмана, -статистич. сумма активир. комплекса. Результаты вычислений k₀ для др. механизмов активации интерпретируют посредством замены Z на PZ, где р-коэф., определяемый механизмом активации и т-рой. Выражение для 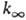не зависит от механизма активации.

Константы 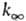и k₀ вычисляют с точностью в среднем до множителя 3-10. Погрешность в осн. связана с неопределенностью исходных данных о k (Е, Е)и 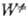(Е — D), ведущей к погрешностям вычислений соотв. b и 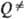. Удовлетворит. результаты удается получить путем коррекции множителей b и 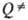по эксперим. данным с о₀ 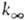и при одном значении т-ры (или в узком интервале т-р). Сравнение результатов вычислений с экспериментом показывает, что р слабо уменьшается с возрастанием т-ры, а при ~ 1000 К, как правило, по порядку величины р составляет 0,1. Это свидетельствует о значит. отклонении механизма активации от механизма сильных столкновений.

Дальнейшее развитие теории связано с исследованиями возможных динамич. ограничений, налагаемых на перераспределение энергии и на скорость самопроизвольного превращ. активной молекулы, более точным количеств. определением k(E,E)на основе эксперим. данных об эффективных сечениях передачи энергии при столкновениях или квантовомех. расчетов. Наряду с аналит. подходами к решению этих вопросов быстро развиваются методы численного моделирования на ЭВМ процессов внутримолекулярного движения, активации и дезактивации. Как правило, моделирование проводится в рамках классич. механики.

Совр. практика ставит и принципиально новые задачи-изучение кинетики М. р. в неравновесных условиях или при неравновероятном распределении заданной энергии по разл. группам степеней свободы реагирующей молекулы. Такие условия реализуются, напр., при избират. воздействии внеш. источников энергии на нeк-рые степени свободы молекулы (возбуждение колебат. состояний молекулы электронным ударом в плазме электрич. разряда, ИК излучением лазера и т.д.) в быстрых газодинамич. процессах (сжатие в ударных волнах, истечение газа из сопла в разреженное пространство и др.). Подобные задачи не м. б. решены в рамках статистич. теории и требуют более детального изучения в кинетике М.р. роли разл. видов внутримолекулярного движения (колебаний определенного типа, вращений, электронного возбуждения) и разл. процессов передачи энергии при столкновениях. В ряде случаев кинетику М.р. удается исследовать в рамках обобщенной статистич. теории путем представления неравновесной среды или системы колебат. и вращат. степеней свободы молекулы в виде неск. подсистем, каждая из к-рых характеризуется своим значением т-ры (см. Неравновесная химическая кинетика ).

Лит.: Робинсон П., Холбрук К., Мономолекулярные реакции, пер. с англ., М., 1975; Кузнецов Н. М., Кинетика мономолежуллрных реакций, М., 1982. Я. М. Кузнецов.