Химическая энциклопедия

АКТИВИРОВАННОГО КОМПЛЕКСА ТЕОРИЯ (теория переходного состояния, теория абс. скоростей р-ций), простейший и исторически первый вариант статистич. теории хим. р-ций. Разработана Э. Вигнером, М. Поляни, Г. Эйрингом, М. Эвансом в 30-х гг. 20 в. Позволяет приближенно рассчитывать скорость элементарных термич. хим. р-ций, исходя из электронного строения и св-в молекул реагентов. В основе теории лежит фундаментальное для химии понятие многомерной поверхности потенциальной энергии (ППЭ) р-ции. Для микроскопия, системы частиц (атомов, молекул), между к-рыми может происходить р-ция (в дальнейшем такую систему будем называть химической), ППЭ - ф-ция потенциальной энергии атомных ядер U от их внутр. координат, или степеней свободы. В системе из п ядер число внутр. степеней свободы N = 3n — 6 (или 3n — — 5, если все ядра расположены на одной прямой линии). Простейшая двухмерная (N = 2) ППЭ показана на рис. 1. Реагентам и продуктам р-ции на ней соответствуют области относительно небольшой потенциальной энергии (долины), разделенные областью повыш. энергии-потенциальным барьером. Кривая линия, проходящая по дну долин через барьер,-координата реакции . Часто используют одномерные схемы, изображающие сечение ППЭ, развернутое вдоль координаты р-ции (см. рис. 2). На этих схемах вершине потенциального барьера соответствует седло-вая точка, или точка перевала. Эти же понятия переносят на многомерные ППЭ с 2>N > 2 . Состояния реагентов и продуктов устойчивы, им соответствуют конфигурации (т.е. фиксированные значения координат ф), к-рые являются минимумами (или долинами) на многомерной ППЭ. Хим. р-ция рассматривается как переход из конфигурации реагентов в конфигурацию продуктов через конфигурацию седловой точки вдоль координаты р-ции. Конфигурации как минимумов, так и седловых точек-стационарные точки ППЭ, т.е. в нихU/q_i = 0.

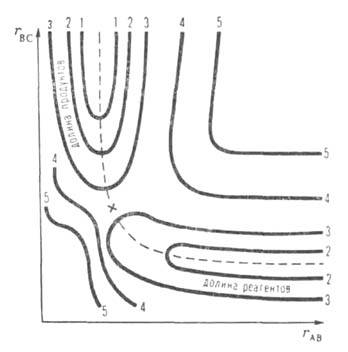
Рис. 1. AB + C ПP PACПOЛOЖEH BCEX TPEX ATOM A>Простейшая ППЭ для р-ции А + ВС -> АВ + С при расположении всех трех атомов А, В и С на одной прямой (угловые движения игнорируются). По координатным осям отложены межатомные расстояния r_BC и r_АВ- Кривые 1-5-уровни постоянной энергии (в условных единицах). Пунктиром обозначена координата р-ции, крестом-седловая точка.

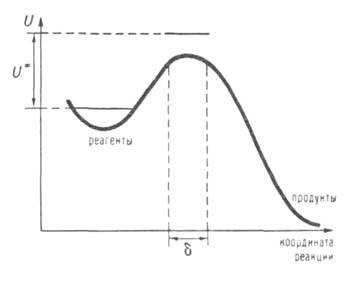
Рис. 2. Профиль ППЭ вдоль координаты р-ции. Вертикальные пунктирные линии ограничивают область, соответствующую активированному комплексу на координате р-ции (ее размер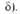 Горизонтальные сплошные линии-нулевые колебат. уровни энергии для реагентов и комплекса.

А. к. т. исходит из предположения о том, что скорость р-ции определяется св-вами нек-рой выделенной геом. конфигурации хим. системы. Обычно принимают, что эта конфигурация соответствует седловой точке на ППЭ; ее наз. активированным комплексом (АК), или переходным состоянием. На одномерной схеме (см. рис. 2) границы конфигурации АК определяются произвольно малой длиной 5 вблизи вершины барьера.

Уравнение для скорости реакции. В седловой точке ППЭ с координатами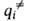(i = 1, 2, ..., N)все первые производные ф-ции U(q_i)равны нулю, так что разложение ф-ции по отклонениям (q_i —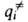) начинается с квадратичных членов. Это означает, что для АК можно определить N нормальных колебаний (мод), как и для обычных устойчивых молекул, а также ввести вращат. и постулат. степени свободы, характеризующие движение АК как целого. Однако в отличие от устойчивой молекулы, к-рой соответствует на ППЭ не сед-ловая точка, а минимум, для АК одна из нормальных мод, а именно движение вдоль координаты р-ции, приводит к его распаду; частота этой моды-чисто мнимая величина. Неустойчивая конфигурация АК характеризуется временем жизни:

где k и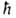-постоянные Больцмана и Планка соотв., Т-абс. т-ра. При обычных для хим. р-ций т-рах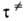~10^-13с.

А. к. т. постулирует термодинамич. равновесие между реагентами и АК, характеризуемое константой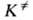. На этом основании константа скорости хим. р-ции к выражается ур-ниями:

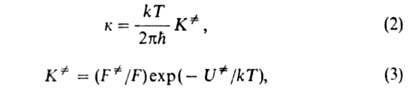
где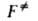 и F-отнесенные к единице объема статистич. суммы АК и реагентов соотв.,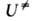-изменение потенциальной энергии системы при переходе от реагентов к АК. Величина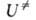складывается из высоты потенциального барьера и разности нулевых колебат. энергий АК и реагентов (см. рис. 2). В ф-ле (3) она приведена в расчете на 1 АК; обычно же ее относят к N_A = 6,02*10²³ АК; тогда в показателе экспоненты k заменяют газовой постоянной R. При вычислении статистич. суммы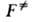 учитывают все степени свободы АК, кроме движения по координате р-ции, а именно постулат. и вращат. движения АК как целого и (N — 1) остальных колебаний, наз. поперечными.

В ранних формулировках А. к. т. гипотеза о равновесии между реагентами и АК трактовалась буквально и к при равнивалась произведению частоты распада АК 1/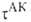 на константу равновесия К :

Величины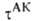 и К^АК вычисляются обычными методами статистич. механики; обе они пропорциональны длине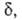 определяющей границы конфигурации АК на координате р-ции. Поскольку их отношение (4) не зависит от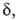 эти границы условны, ур-ния (2) и (3) получаются из (4) при произвольном выборе значения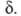Выражение К через статистич. суммы аналогично ф-ле (3), но вместо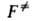 используют полную статистич. сумму АК F = f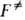, где f -элементарная статистич. сумма для движения системы вдоль координаты р-ции; именно она пропорциональна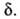Можно ввести спец. определение АК, выбрав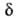т. обр., чтобы для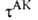 и К получились в точности выражения (1) и (3), т.е. 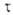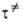положив^АК = и К^АК =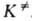. При этом f= 1 и F^AK =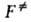. Тогда термодинамич. интерпретация ур-ния (2) становится особенно наглядной; соответствующее значение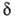 составляет ок. 1 нм.

Рассматривая в (3)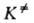как константу равновесия, можно представить (2) в термодинамич. форме:

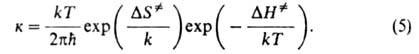
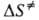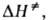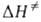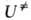Величины иназ. соотв. энтропией и энтальпией активации, представляют собой изменения энтропии и энтальпии системы при переходе от реагентов к АК. Как правило, осн. вклад в дает, а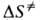 определяется в осн. статистич. суммами: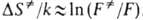; исключением м.б. р-ции в полярных р-рителях. Ур-ния (2) и (3) применяют к газофазным р-циям, а (5)-для расчета скоростей р-ций в р-рах, когда вычисления статистич. сумм затруднительны. Соотв. предполагается, что в первом случае р-ция протекает при постоянном объеме, во втором-при постоянном давлении.

Совр. вывод ур-ния (2), химически менее наглядный, основан на столкновений теории . Скорость р-ции отождествляется со скоростью перехода реагирующих хим. систем через (N — 1 )-мерную пов-сть в пространстве конфигураций, разделяющую области реагентов и продуктов. В теории столкновений эта скорость наз. потоком через критич. пов-сть. Ур-ние в форме (2) получается, если провести критич. пов-сть через седловую точку ортогонально координате р-ции и принять, что на критич. пов-сти энергетич. распределение реагентов равновесно. Соответствующая область пространства координат и импульсов (фазового пространства) характеризуется той же статистич. суммой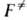 . Это позволяет рассматривать критич. пов-сть как множество конфигураций АК. Т. обр., АК сразу определяется как объект с (N — 1) внутр. степенями свободы и не нужно вводить его протяженность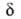 вдоль координаты р-ции.

Применение теории. Согласно теории, механизм р-ции вполне определен конфигурациями реагентов и продуктов (минимумы, или долины, на ППЭ) и соответствующих АК (седловые точки). Теоретич. расчет этих конфигураций методами квантовой химии дал бы исчерпывающую информацию о направлениях и скоростях хим. р-ций. Такие расчеты интенсивно развиваются; для простых хим. систем, содержащих 10-15 атомов, к-рые принадлежат к элементам первых двух периодов таблицы Менделеева, они практически реализуемы и достаточно надежны. Последоват. расчет абс. скорости р-ции по ур-нию (2) заключается в определении геом. конфигураций реагентов и АК (на этом этапе также определяется высота потенциального барьера) и вычислении для этих конфигураций моментов инерции и колебат. частот, к-рые необходимы для расчета статистич. сумм и окончат. определения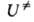. В применении к сложным р-циям, представляющим практич. интерес, полная и надежная реализация такой программы трудоемка и зачастую неосуществима. Поэтому молекулярные постоянные, необходимые для вычислений по ур-ниям (2) и (3), часто находят эмпирич. методами. Для устойчивых конфигураций реагентов моменты инерции и колебат. частоты обычно известны из спектроскопич. данных, однако для АК эксперим. определение их невозможно ввиду малого впемени его жизни. Если последоват. квантовохим. расчет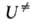и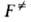 недоступен, для оценки этих величин применяют интерполяционные расчетные схемы.

А. к. т.-основа качеств. представлений о реакц. способности в-в. Ур-ния (2), (3) и (5) имеют ту же форму, что и ур-ние Аррениуса, к-рое эмпирически описывает температурную зависимость кинетич. констант разл. хим. процессов. Величину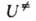 во мн. случаях достаточно отождествить с наблюдаемой энергией активации, пренебрегая слабой (по сравнению с экспоненциальной) температурной зависимостью статистич. сумм и множителя k Т/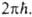 Тогда пред-экспоненциальный множитель в ур-ниях (2) и (3) можно отождествить с аррениусовским. Его значение слабо зависит от деталей строения АК и оценка по порядку величины не составляет труда. Оказывается, что в реакц. сериях с одинаковым реакц. центром предэкспоненциальный множитель примерно постоянен, т.е. ряды активности определяются значениями энергии активации. Наконец, если пренебречь вкладом нулевых колебат. энергий в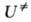, высота потенциального барьера р-ции становится единственной фундам. характеристикой ее скорости. Для теоретич. оценки относит. изменений высоты потенциального барьера в реакц. сериях разработаны простые методы (см. Реакционная способность ). Такой подход к оценке относит. скоростей применяют для любого физ.-хим. процесса, если высота потенциального барьера, разделяющего исходное и конечное состояния, достаточно высока по сравнению с kT; он не требует громоздких вычислений и широко распространен. Именно этим определяется плодотворность и универсальность концепции АК в теоретич. химии.

Ограниченность теории и попытки ее совершенствования. А. к. т. основана на двух предположениях. Первое-гипотеза о термодинамич. равновесии между реагентами и АК. Согласно второму, скорость р-ции отождествляется со скоростью распада АК. Оба предположения нельзя строго обосновать. Это обнаруживается, если рассматривать движение хим. системы вдоль координаты р-ции на всем пути от реагентов к продуктам, а не только вблизи вершины потенциального барьера. Координату р-ции лишь в редких случаях правильно считать прямой линией, как на рис. 2. Обычно же она-кривая в многомерном пространстве внутр. переменных и является сложной комбинацией элементарных движений, к-рая неодинакова на разл. своих участках. Напр., на рис. 1 координата р-ции-это непрерывно изменяющаяся комбинация двух валентных колебаний.

Равновесное распределение энергии в реагентах для термич. р-ций обеспечено практически всегда; оно нарушается только в чрезвычайно быстрых процессах. Проблема в том, сохранится ли оно в АК. Из-за криволинейности координату р-ции нельзя считать независимой степенью свободы. Ее взаимод. с другими, поперечными движениями приводит к обмену энергией между ними. В результате, во-первых, может нарушиться первоначально равновесное распределение энергии по поперечным степеням свободы и, во-вторых, система может вернуться в область реагентов даже после того, как она уже прошла через конфигурацию АК в направлении продуктов. Наконец, необходимо иметь в виду, что, согласно ур-ниям (2), (3) и (5), хим. р-ция рассматривается как классич. переход; игнорируются квантовые особенности, напр. электронно-неадиабатич. процессы и туннельный эффект. В ранних формулировках теории в ур-ния (2), (3) и (5) добавляли т. наз. трансмиссионный множитель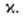Предполагалось, что в нем собрано влияние перечисленных выше факторов, не учтенных при выводе этих ур-ний. Т. обр., определение х выходит за рамки А.к.т.; более того, для р-ций, в к-рых х значительно отличается от единицы, теория теряет смысл. 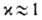Однако для сложных р-ций предположение не противоречит экспе-рим. данным, и именно этим объясняется популярность А. к. т.

Последоват. неформальное рассмотрение всех указанных эффектов возможно лишь в рамках динамич. расчета (см. Динамика элементарного акта ). Предпринимались попытки учесть их по отдельности. Напр., был предложен метод си-стематич. уточнения конфигурации АК, поскольку выбор в кач-ве таковой именно седловой точки основан на интуитивных представлениях и, вообще говоря, не обязателен. Могут существовать и др. конфигурации, для к-рых погрешность вычислений по ф-лам (2) и (3), обусловленная возвращением системы в область реагентов после прохождения этих конфигураций, меньше, чем для конфигурации седловой точки. Используя формулировку А. к. т. в терминах теории столкновений (см. выше), можно утверждать, что обратному потоку (от продуктов к реагентам) через критич. пов-сть соответствует порождающая его и равная ему часть полного прямого потока (от реагентов к продуктам). Чем меньше эта часть, тем точнее вычисление скорости р-ции по А. к. т. Эти соображения легли в основу т. наз. вариационного определения АК, согласно к-рому критической считается пов-сть, минимизирующая прямой поток. Для нее скорость р-ции, вычисляемая по ур-ниям (2) и (3), минимальна. Как правило, нулевые энергии поперечных колебаний изменяются вдоль координаты р-ции. Это еще одна причина смещения конфигурации АК из седловой точки ППЭ; она также учитывается вариационной теорией.

Значит. внимание уделялось разработке методов определения вероятностей квантового туннелирования в хим. р-циях. Наконец, стали возможны оценки трансмиссионного множителя в рамках модельных динамич. вычислений. При этом предполагается, что с постулат. движением системы вдоль координаты р-ции взаимодействуют не все, а лишь нек-рые из поперечных степеней свободы. Они и учитываются в квантовом динамич. расчете; остальные степени свободы обрабатываются в рамках равновесной теории. При таких вычислениях автоматически определяются также и поправки на квантовое туннелирование.

Упомянутые усовершенствованные методы расчета абс. скоростей хим. р-ций требуют серьезных вычислит. усилий и лишены универсальности А. к. т.

Лит.: Глесстон С, Лейдлер К., Эйринг Г., Теория абсолютных скоростей реакций, пер. с англ., М., 1948; Лейдлер К., Кинетика органических реакций, пер. с англ., М., 1966: Термические бимолекулярные реакции в газах, М., 1976. М. В. Базилевский.