Химическая энциклопедия

РЕАКЦИОННАЯ СПОСОБНОСТЬ , характеристика относительной хим. активности молекул, атомов, ионов, радикалов. Для количеств. оценки Р.с. рассматривают реакционные серии, т.е. ряды однотипных р-ций, проводимых в одинаковых условиях, напр.: (стандартная р-ция)

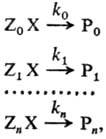
где Х-общая группа атомов, к-рая претерпевает изменения в данной р-ции (реакционный центр), Z₀, Z_l,..., Z_n-неизменяющиеся мол. фрагменты, Р₀, Р₁,..., Р_n -продукты р-ции. Отношения констант скоростей k₁/k₀,..., k_n/k₀ количественно характеризуют Р. с. в ряду реагентов Z_iX (i = 0, 1, ..., п). В правильно составленной реакц. серии изменение механизма реакции должно быть исключено, т. е. константы скорости должны характеризовать одну и ту же элементарную р-цию.

Типичные реакционные серии. Простейшая ситуация возникает при анализе изомерного состава продуктов р-ции. В р-ции электроф. замещения в ароматич. ряду в зависимости от заместителя R образуются те или иные изомеры, напр. при нитровании:

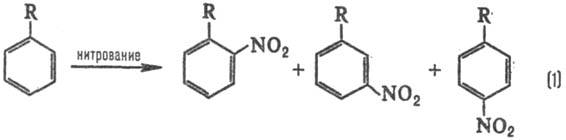
Электронодонорные заместители [R=СН₃, ОСН₃, N(CH₃)₂] стимулируют образование орто- и пара -продук-тов, а электроноакцепторные (R = СООН, SO₃H, NO₂)-мета -продуктов, причем в первом случае р-ция идет легче, чем с незамещенным бензолом (R = Н), а во втором-труднее. Эти закономерности наз. правилами ориентации в ароматическом ряду. При нуклеоф. замещении правила ориентации обращаются.

Стереохим. направленность перипиклич. р-ций определяется Вудворда-Хофмаиа правилами, напр.:

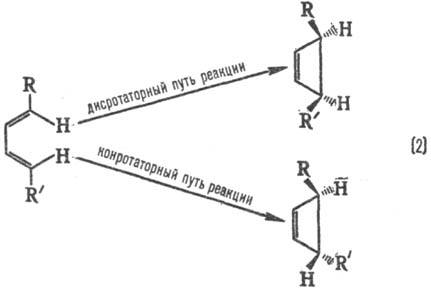
При дисротаторном пути р-ции заместители R и R в продукте будут расположены по одну сторону плоскости цикла, при конротаторном пути-по разные стороны. Эксперимент показывает, что термич. циклизация производных бутадиена происходит по конротаторному пути, а фотохим. циклизация-по дисротаторному пути.

В примерах (1) и (2) нет необходимости в количеств. кинетич. измерениях, Р. с. определяется по относит. выходу изомеров. Пример широкой реакц. серии-р-ции радикального присоединения по двойной связи:

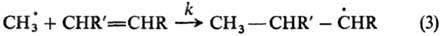
Р. с. характеризуется отношением константы скорости k к константе скорости k₀ р-ции с этиленом (R, R = Н) (см. табл.). Аналогичные кинетич. измерения сделаны для р-ций присоединения метильного радикала к ароматич. молекулам и для р-ций присоединения др. радикалов.

Квантовохимическая теория Р.с. Совр. теоретич. химия позволяет непосредственно рассчитать абс. константы скорости только для несложных хим. систем. В теории Р. с. качеств. закономерности м.б. выявлены для объектов любой сложности. При этом используют разл. подходы. При эмпирич. подходе классифицируют влияние заместителей по неск. типам (эффекты сопряжения, полярные, пространственные и др.) и применяют корреляционные соотношения . Традиц. квантовохим. подход основан на активированного комплекса теории ; при этом предполагается, что для всех р-ций, составляющих реакц. серию (без пространств. и соль-ватац. эффектов), остается примерно постоянным пред-экспоненц. множитель А в Аррениуса уравнении для константы скорости k = Aexp(-E ^./RT) (R-газовая постоянная, Т-абс. т-ра). Поэтому характеристикой Р.с. служит энергия активации р-ции E^., к-рая практически совпадает с высотой потенц. барьера на поверхности потенциальной энергии (ППЭ).

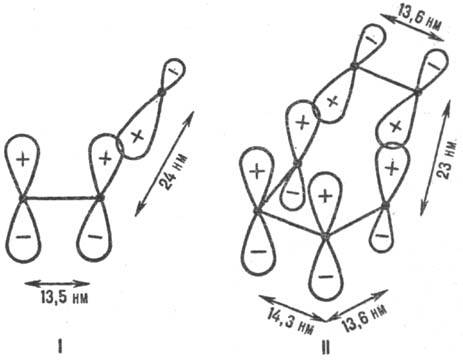
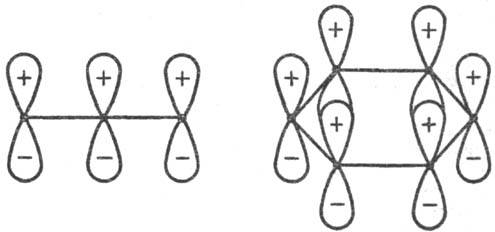
Рис. 1. Переходные состояния р-ций присоединения с участием p-электронных систем. I-радикальное присоединение (метальный радикал + этилен), II-р-ция Дильса-Альдера (этилен + бутадиен); внизу изображены соответствующие модельные p-сопряженные структуры. Показаны атомные 2p_p-орбитали, асимметрия к-рых обусловлена изменением гибридизации вследствие взаимод. в переходном состоянии. Черные точки-ядра атомов С. Знаки " + " и " —" относятся к соответствующим волновым ф-циям. Орбитали перекрываются в фазе. Приведены межатомные расстояния в переходном состоянии.

Энергия стабилизации. Для относит. оценки E^. в реакц. сериях важна концепция делокализации электронов в переходном состоянии (активир. комплексе) р-ции (М. Эванс, 1939). Согласно этой концепции, электронное строение мн. реакц. центров подобно строению сопряженных открытых и циклических я-электронных систем (рис. 1). Открытое переходное состояние радикальной р-ции типа (3) подобно p-электронной системе аллильного радикала (рис. 1, I), а "циклическое" переходное состояние согласованной р-ции Дильса-Альдера (этилен + бутадиен) по строению напоминает бензол (рис. 1, И). p-Электроны заместителей R и R включаются в общую делокализованную систему электронов. Относит. мерой энергии активации р-ции, а следовательно и Р. с., может служить энергия стабилизации переходного состояния (энергия делокализации), т.е. разность между энергией сопряженной системы p-электронов переходного состояния и энергией p-электронов в изолир. реагентах. Энергию стабилизации можно рассчитать полу-эмпирическими методами квантовой химии, напр. методом Хюккеля. Вычисляя энергию стабилизации, можно предсказывать Р. с. хим. соединения во мн. р-циях (иллюстрации см. на рис. 2).

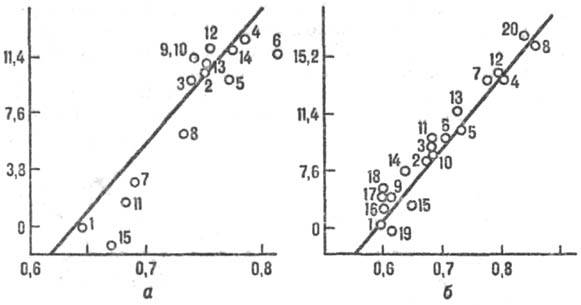
Рис. 2. Корреляция между реакц. способностью и энергией стабилизации переходного состояния, а-р-ции присоединения метального радикала СН^•₃ к олефи-нам, цифры соответствуют номеру олефина в таблице. На оси ординат отложены величины 2,3 RТ lg k/k₀ (кДж/моль), где k/k₀ - отношение констант скорости рассматриваемой р-ции и р-ции с этиленом, R-газовая постоянная, Т-абс. т-ра. На оси абсцисс отложены энергии стабилизации в относит единицах, б-р-ция СН^•₃ + ароматич. молекула. В скобках указано положение в молекуле субстрата, для к-рого приводится константа k. k₀- константа скорости р-ции с бензолом. 1-бензол; 2-нафталин (1); 3-фенантрен (9); 4-антрацен (9); 5-пирен (1); 6-хризен (6); 7-бенз(а)антрацен (7); 8-нафтацен (5); 9-пиридин (2); 10-хино-лин (4); 11 -изохинолин (1); 12-акридин (9); 13-феназин (1); 14-бензонитрил (4); 15-ацетофенон (4); 16-фторбензол (4); 17-хлорбензол (4); 18-бромбензол (4); 19-анизол (4); 20-бензохинон.

Концепция граничных орбиталей. Оценки Р.с. особенно просты, если использовать возмущений теорию . В распространенном варианте теории возмущений энергия стабилизации представляется в виде суммы вкладов от взаимод. между мол. орбиталями реагентов. Наиб. вклад в сумму дают, как правило, взаимод. граничных орбиталей, т.е. высших заполненных электронами и низших незаполненных орбиталей; согласно К. Фукуи (1952), существенны только эти вклады (см. Граничных орбиталей теория ). Концепцию граничных орбиталей часто применяют в качестве основы для обсуждения Р. с.

Альтернантные системы. Качеств. подход, не обязательно использующий теорию возмущений, сформулирован для класса сопряженных систем, наз. альтернант-ными. Они образованы из одинаковых атомов (обычно углерода) и не содержат нечетных циклов (см. Альтернантные углеводороды ). Для таких систем в рамках Хюккеля метода можно без всяких вычислений выявить нек-рые общие закономерности. Так, введение полярного заместителя приводит к чередованию положит. и отрицат. изменений электронной плотности в сопряженной углеродной цепи относительно незамещенного углеводородного соед. (закон альтернирующей полярности, Ч. Коул-сон, Г. Лонге-Хиггинс, 1947). Этот вывод теории позволяет объяснить правила ориентации в ароматич. ряду (р-ция 1).

Для циклич. переходного состояния (активир. комплекса) существенно, каким образом замыкаются новые связи: в фазе или в противофазе, т.е. имеют ли атомные орбитали реагентов в области макс. перекрывания одинаковые или противоположные знаки (рис. 1 и 3). В первом случае взаимод. наз. связывающим, во втором-разрых-ляющим. В зависимости от числа атомных орбиталей в сопряженной системе активир. комплекса, электронного состояния реагирующей системы и характера вновь возникающих взаимодействий, энергия замыкания цикла м. б. как положительной, так и отрицательной, причем ее знак определяется без вычислений. В частности, при циклизации производных бутадиена (р-ция 2) в основном электронном состоянии переходное состояние стабилизируется замыканием связей посредством разрыхляющих взаимод. (перекрывание в противофазе, рис. 3), делая энергетически выгодным конротаторный путь термич. р-ции. В первом электронном возбужденном состоянии циклич. переходное состояние стабилизируется связывающим взаимод. (перекрывание в фазе), что соответствует дисротаторному пути. Эти общие положения позволяют предсказывать закономерности Р. с. согласованных электроциклич. р-ций (Р. Вуд-ворд, Р. Хофман, 1965).

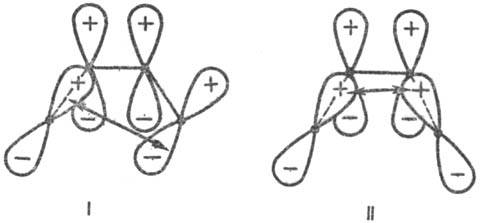
Рис. 3. Переходные состояния р-ции циклизации производных бутадиена. I-конротаторный путь р-ции (орбитали вновь образующейся связи перекрываются в протпвофазе); II-дисротаторный путь р-ции (орбитали перекрываются в фазе). Обозначения те же, что и на рис. 1. Стрелки указывают области наилучшего перекрывания атомных орбиталей реакц. центра.

Индексы Р. с. - теоретич. величины, к-рые используют для характеристики Р.с. на простом модельном уровне и обычно рассчитывают квантовохим. методами. Один из индексов Р. с.-энергия стабилизации; др. индексы менее универсальны, часто они являются приближенными оценками энергии стабилизации применительно к конкретным типам р-ций. Так, в случае ионных р-ций с участием p-элект-ронных систем в качестве индексов Р.с. применяют p-электронные поляризуемости (для углеводородных субстратов) и p-электронные эффективные заряды атомов (для углеводородных субстратов с полярными заместителями или для гетероциклич. субстратов). В случае радикальных р-ций присоединения в качестве индексов Р.с. особенно подходящи энергии локализации, а также индексы своб. валентности. В частности, опытные константы скорости присоединения метильного радикала к олефинам и ароматич. молекулам (рис. 2) удовлетворительно коррелируют с энергиями локализации. Совр. развитие представлений об индексах Р. с. связано с т. наз. теорий функционала плотности, согласно к-рой для квантовомех. описания электронного строения мол. систем вместо волновой ф-ции используется ф-ция электронной плотности (Р. Парр, В. Янг, 1989).

Индексы Р. с. применимы в тех случаях, когда хим. перестройка затрагивает в осн. p-электронные системы реагентов. Если же наряду с p-электронной системой значительно перестраиваются и s-связи реагентов, применение p-электронного приближения мало эффективно. В подобных случаях, а также если в реагирующих системах вообще нельзя выделить систему p-электронов, изменения энергий активации р-ций, составляющих реакц. серию, оцениваются с помощью полуэмпирич. или неэмпирических методов квантовохим. вычислений в рамках разл. моделей р-ции, учитывающих все валентные электроны. В результате получают индексы Р. с., к-рые при подходящем выборе модели удовлетворительно коррелируют с кинетич. изменениями. Такое квантовохим. описание утрачивает качеств. наглядность p-электронной модели.

Соотношение Брёнстеда [Бренстеда]. Если простые квантовохим. методы неэффективны, Р. с. часто интерпретируют с помощью определяемых на опыте корреляций между логарифмами констант скорости k_i и констант равновесия К_i р-ций, образующих реакц. серию. Такие же корреляции существуют между энергиями активации Е_i^. и тепловыми эффектами р-ций Q_i (рис. 4). В предположении о постоянстве пред-экспоненц. множителя в ур-нии Аррениуса для k_t оба типа корреляций эквивалентны. Типичные примеры-р-ции переноса атома водорода или протона:

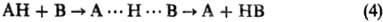
(В и А-радикалы или анионы; А···H···В-делокализован-ная структура переходного состояния) и р-ции нуклеоф. замещения S_N2:

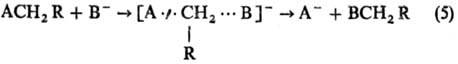
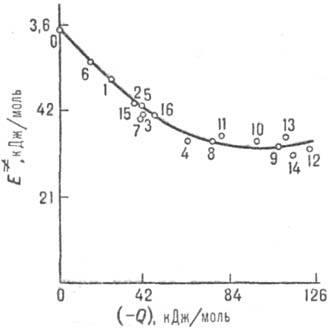
Рис. 4. Корреляция между энергией активации E^. и тепловым эффектом Q для газофазных р-ций отрыва атома Н метильным радикалом СН^•₃. 0-метан; 1-этан; 2-пропан; 3 - бутан; 4 - изобутап; 5 - неопентан; 6 - циклопропан; 7-циклогексан; 8-пропилен; 9-изобутен; 10-транс- 2-бу-тей; 11 - толуол; 12 - о-ксилол; 13- м- ксилол; 14-n-ксилол; 15-метанол; 16-ацетон.

Корреляции такого рода часто описывают уравнением Маркуса:

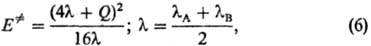
где l_А и l_B-параметры, наз. "внутренними барьерами" реагентов А и В. Ур-ние (6) предполагает нелинейную (квадратичную) зависимость между Е^. и Q. Однако во мн. случаях (особенно для ионно-молекулярных реакций в полярном р-рителе) корреляции становятся прямолинейными (рис. 5), т.е. маркусова кривизна брёнстедовских [бренстедовских] графиков исчезает.

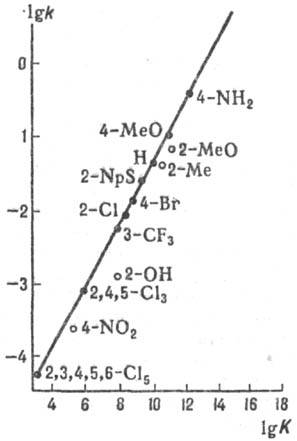
Рис. 5. Корреляция между константами скорости k и константами равновесия К для р-ции S_N2 (5) в диметилсульфоксиде при 25 °С. АСН₂R - бутилхлорид (А = С1), В^- - замещенные фенилтиолят-анионы (указаны заместители), NpS -нафтилтиолят-анион.

В отличие от квантовохим. теорий, объясняющих Р.с. исходя из электронного строения реагентов, соотношение (6) и др. ур-ния такого типа основаны на анализе изменений структуры ППЭ в реакц. серии. Рассматривают смещение положения переходного состояния на координате реакции в зависимости от заместителей. Положение переходного состояния характеризуется безразмерной величиной а, к-рая может принимать значения между нулем (положение реагентов на координате р-ции) и единицей (положение продуктов на координате р-ции). В рамках простейших моделей ППЭ

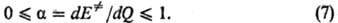
Производную dE^. /dQ находят из соотношений между Е^. и Q типа (6); она наз. брёнстедовским [бренстедовским] коэффициентом. Ф-ла (7) является количеств. формулировкой постулата Хэммонда, утверждающего, что в реакц. серии переходное состояние тем более продвинуто по координате р-ции в направлении продуктов, чем меньше экзотермич-ность р-ции (и чем меньше Р. с.). Известны исключения, т. е. такие реакц. серии, в к-рых неравенства (7) не соблюдаются. Они свидетельствуют о сложности строения соответствующих ППЭ, не учтенной при выводе ф-лы (7).

Влияние среды на Р.с. Совр. развитие теории Р. с. связано с изучением влияния среды на р-ции, протекающие в конденсир. фазе. (См. также Реакции в растворах ). Согласно классич. подходу (С. Глесстон, К. Лейдлер, Г. Эйринг, 1941), определяют изменения энергии начального состояния реагентов и переходного состояния под влиянием среды (р-рителя) в рамках теории активир. комплекса. Роль среды сводится к созданию дополнит. потенциала, модифицирующего ППЭ соответствующей р-ции в газовой фазе. Этот потенциал м.б. учтен в совр. квантовохим. расчете. Модификация ППЭ потенц. полем среды м. б. очень велика для р-ций с переносом заряда в полярном р-рителе, напр. S_N2.

С принципиальной точки зрения наиб. интересны такие хим. р-ции, к-рые сопровождаются перестройкой среды. Их изучение требует от теории явного рассмотрения координат, связанных с изменениями, происходящими в среде. Иногда координата перестройки среды дает осн. вклад в координату р-ции на энергетич. пов-сти вблизи седловой точки, соответствующей переходному состоянию. Это означает, что потенц. барьер преодолевается в осн. за счет движения частиц среды. Типичная модельная р-ция такого типа-внешне-сферный перенос электрона окружении ионов (см. Одноэлектронный перенос ). Перенос электрона фиксируется изменением состояния среды (переход из состояния I в состояние II).

Предполагается, что перенос электрона происходит при фиксир. расстоянии между ионами и не учитываются (в простейшем случае) структурные изменения в лигандном

Для р-ций в полярном р-рителе состояние среды характеризуется ее поляризацией, связанной со средней величиной и ориентацией дипольных моментов молекул р-рителя. Поляризация среды (дипольный момент, отнесенный к единице объема), если среда равновесна, определяется распределением электрич. зарядов в хим. подсистеме и изменяется вместе с ним. Для внешнесферного переноса электрона координата перестройки среды есть коллективная переменная-величина, выражающаяся через поляризацию среды. В более сложных (и химически более интересных) ситуациях координаты перестройки среды и внутр. координаты хим. подсистемы рассматриваются на равных основаниях, т.е. энергетич. пов-сть строится в пространстве координат обоих типов. При этом возможны неравновесные эффекты: если движение системы по координате перестройки среды более медленное, чем движение по "химической" координате, среда не успевает подстроиться под "химическое" движение. Тогда имеет место неравновесная сольватация переходного состояния и теория активир. комплекса не применима, поскольку она основана на предположении о равновесном распределении энергии в переходном состоянии. Р. с. в таких системах коррелирует с динамич. характеристиками среды. Для р-ций с перераспределением заряда в полярном р-рителе динамич. характеристикой среды является время т_L продольной электрич. релаксации (рис. 6). Если же электрич. взаимодействие хим. подсистемы со средой не столь существенно, на первый план выступают эффекты, зависящие от гидродинамич. вязкости h среды или от коэф. диффузии D (рис. 7), обратно пропорционального вязкости (h ~ D^-1). Корреляции Р. с. с динамич. характеристиками среды находят объяснение в рамках стохастич. кинетич. теорий.

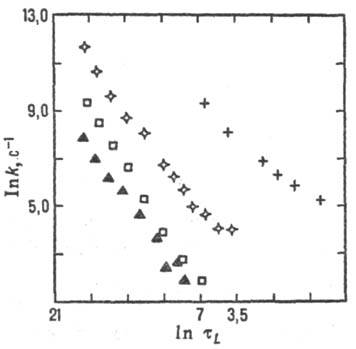
Рис. 6. Корреляция между константами скорости k и временами продольной диэлект-рич. релаксации т_L (р-ция переноса электрона между комплексами рутения и метилвио-летом в глицерине; значки разл. формы относятся к разл. лигандам в комплексе рутения).

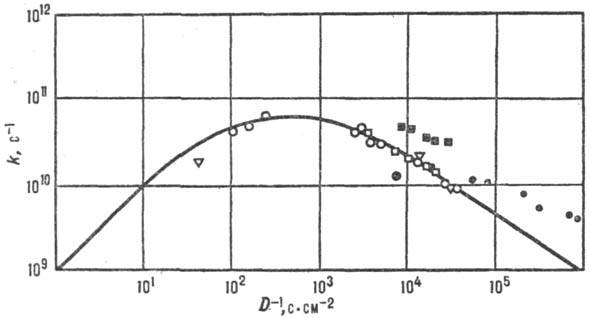
Рис. 7. Корреляция между константами скорости k и козф. диффузии D (фото-хим. изомеризации стильбена в газовой и жидкой фазах при разных давлениях). Значки разл. формы отвечают разным средам; сплошная линия—расчет по ур-нию Крамерса.

Простейшая стохастич. теория, установившая зависимость константы скорости р-ции от вязкости, была разработана Г. Крамерсом (1940). В рамках стохастич. описания энергетика р-ции считается известной и исследование кинетики, если р-ция равновесна, переносится на предэкспоненц. множитель А. Если же р-ция протекает неравновесно, аррениу-совская зависимость константьд скорости р-ции теряет смысл, т. к. энергия активации Е^. и предэкспоненц. множитель зависят от т-ры. Между "эффективными" значениями Е и А часто наблюдаются корреляции (см. Компенсационный эффект ).

Изложенные общие принципы описания влияния среды на Р. с. перспективны для применения к хим. р-циям, протекающим в сложных системах, напр. биологических.

Разобранные примеры свидетельствуют о многообразии проблем, связанных с Р. с. Для простейших реакц. серий достаточны элементарные квантовохим. рассуждения (р-ции 1 и 2). В более сложных случаях для понимания закономерностей Р. с. необходимо привлекать динамич. подходы (см. Динамика элементарного акта ) и методы статистич. физики (пример 8 и рис. 6). Вся совокупность этих проблем и применяемых при их решении методов составляет содержание совр. теории хим. р-ций.

Лит.: Базилевский М. В., Метод молекулярных орбит и реакционная способность органических молекул, М., 1969; Вудворд Р., Хоффман Р., Сохранение орбитальной симметрии, пер. с англ., М., 1971; Гаммет Л., Основы физической органической химии, пер. с англ., М., 1972; Дыоар М. Дж., Догерти Р., Теория возмущений молекулярных орбиталей в органической химии, пер. с англ., М., 1977; Салем Л., Электроны в химических реакциях, пер. с англ., М., 1985; Базилевский М. В., Колдобский С. Г., Тихомиров В. А., "Успехи химии", 1986, т. 55, в. 10, с. 1667-98; The chemical physics of solvation, pt A, ed. by R. R. Dogonadze [a. o.], pt C, ed. by A. A. Kornyshev and I. Ulstrup, Amst, 1985 88. М. В. Базилевский.