Химическая энциклопедия

СЛОЖНЫЕ РЕАКЦИИ . Хим. р-ция реализуется как совокупность множества дискретных актов хим. превращения, в каждом из к-рых участвует лишь одна или небольшое число частиц (молекул, атомов, ионов). Если среди актов р-ции имеются химически различающиеся, то р-ция наз. сложной. К С. р. относят наиб. распространенные классы р-ций-каталитические (см. Катализ ) и цепные реакции .

Из множества актов С. р. можно выделить химически одинаковые; они составляют элементарную р-цию. С. р. представляет собой совокупность элементарных р-ций, природа и последовательность к-рых составляют механизм реакции .

Всякая элементарная р-ция в принципе обратима, т.е. всегда наряду с ней возможна р-ция, отличающаяся лишь направлением превращения (см. Обратимые и необратимые процессы ). Совокупность элементарной р-ции и обратной ей в составе С.р. наз. стадией С. р. Скорость u_-s обратной р-ции м. б. пренебрежимо мала по сравнению со скоростью u_s прямой р-ции, в таком случае s- ю стадию считают необратимой. Если, напротив, u_s = u_-s (или u_s ! u_-s), s- я стадия равновесна (квазиравновесна, если u_s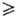u_-s). По характеру взаимосвязи элементарных р-ций выделяют последовательные р-ции (продукт предыдущей элементарной р-ции является исходным в-вом последующей), параллельные р-ции (одновременно протекающие элементарные р-ции, в к-рых по крайней мере одно из исходных в-в общее), последовательно-параллельные р-ции, р-ции с циклич. стадиями и т.п.

Согласно детального равновесия принципу , состояние хим. равновесия при С. р. осуществляется таким образом, что каждая стадия строго равновесна. При удалении реагирующей системы от равновесия стадии С. р. одна за другой становятся вначале неравновесными, а затем и необратимыми.

Итог С. р. передается одним или неск. линейно независимыми хим. ур-ниями (стехиометрич. ур-ниями). В-ва, фигурирующие лишь в хим. ур-ниях стадий С. р., но не в итоговом ур-нии, наз. промежуточными. Итоговое хим. ур-ние С. р. может быть получено сложением хим. ур-ний стадий, умноженных на рациональные числа (положит., отрицат. или равные нулю). Эти числа наз. стехиометрич. числами С.р. Набор стехиометрич. чисел, обеспечивающий получение итогового ур-ния (т.е. приводящий к исключению промежут. в-в), задает маршрут р-ции. М.б. образован базис маршрутов, т.е. такая совокупность маршрутов, что они линейно независимы, т.е. любой иной маршрут данной р-ции является линейной комбинацией ее базисных маршрутов. При каждом механизме р-ции число базисных маршрутов определенно, но выбор их в известной мере произволен. Число базисных маршрутов P больше или равно числу Q независимых итоговых ур-ний. Если P > Q, всегда можно выбрать базис маршрутов таким образом, что итоговым ур-нием (Р — Q) базисных маршрутов С. р. будет 0 = 0; такие маршруты наз. пустыми, а базис, состоящий из Q непустых маршрутов и (Р — Q) пустых,-стехиометрическим.

Чтобы определить кинетику С.р., т.е. представить скорости ее по итоговым ур-ниям в виде ф-ции концентраций исходных в-в и продуктов, нужно из системы ур-ний, получаемой применением действующих масс закона к элементарным р-циям, исключить неизвестные концентрации промежут. в-в. Эта задача упрощается, если р-ция строго стационарна или если ее с достаточным приближением можно считать квазистационарной: вместо системы дифференц. ур-ний имеем тогда систему алгебраич. ур-ний, все производные концентрации промежут. в-в по времени равны нулю (см. Квазистационарности приближение ). С др. стороны, исследуя нестационарную кинетику, можно получить больше информации о механизме С. р., чем если ограничиться лишь стационарной кинетикой.

Условие стационарности С. р. записывается в виде:

где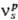-стехиометрич. число s- й стадии по р- му базисному маршруту, u^p-C. p. по этому маршруту, (u_s — u_-s)-Скорость s-и стадии. Ур-ния вида (1) справедливы для каждой стадии, следовательно, их число равно числу стадий S. К этим ур-ниям м.б. прибавлены линейные ур-ния, связывающие концентрации промежут. в-в. Напр., при гетерог. каталитич. р-ции сумма доли пов-сти, покрытой адсорбир. в-вами, и доли своб. пов-сти равна 1. Такие ур-ния наз. балансовыми, их число W. Число неизвестных скоростей по базисным маршрутам, равное Р, и концентрации промежут. в-в I (считая промежут. в-вом и своб. пов-сть) равно числу ур-ний:

Система ур-ний, к-рые получаем, выразив в (1) u_s и u_-s по закону действующих масс, определяет все неизвестные.

Ур-ние (2) позволяет легко определить число базисных маршрутов данной р-ции. Если к.-л. стадия С. р. равновесна, ур-ние (1) в применении к этой стадии заменяется ур-нием, выражающим закон действующих масс для соответствующего равновесия. Для С. р., описываемой неск. итоговыми ур-ниями, достаточно записать кинетич. ур-ния, выражающие скорости по непустым маршрутам стехиометрич. базиса (скорости по пустым маршрутам не требуются, хотя они и не равны нулю).

Альтернативное выражение условий стационарности С. р. имеет вид:

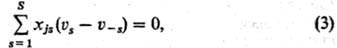
где x_js-стехиометрич. коэф. промежут. в-ва номеру в хим. ур-нии 5-й стадии (положит. число, если в-во образуется, и отрицательное, если в-во расходуется). Условия (1) и (3) эквивалентны, иногда удобнее пользоваться одним, иногда-другим.

В случае одномаршрутной С. р. (р-ции с одним базисным маршрутом) ее стационарная скорость u м.б. выражена через скорости в прямом направлении u₊ и в обратном направлении u_:

при этом

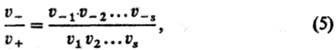
где u₁, u₂, ...-скорости элементарных р-ций всех стадий. Равенство (5) справедливо независимо от того, каковы стехиометрия, числа стадий. Из него следует, что если хотя бы одна стадия необратима, то u_-=0, т.е. С.р. в целом необратима. С помощью изотопных индикаторов можно в ряде случаев определить отдельно u₊ и u_- .

Если все стадии одномаршрутной С. р., кроме одной (номер l), равновесны, то равенство (5) дает: u_-/u₊ ! u_-l/u_l. Тогда, согласно (4), u₊ ! u_l, u_-! u_-l. Такую стадию называют скоростьопределяющей или лимитирующей. Если С. р. проходит в условиях, близких к равновесным, обычно неравновесна лишь одна стадия, она определяет скорость С. р., если р-ция одномаршрутна. М. И. Темкин.