ТЕПЛОЕМКОСТЬ
, кол-во
теплоты, затрачиваемое для изменения т-ры на 1 °С. Согласно более строгому
определению, Т.-термодинамич. величина, определяемая выражением:
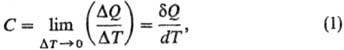
где DQ- кол-во
теплоты, сообщенное системе и вызвавшее изменение ее т-ры на DТ. Отношение
конечных разностей DQ/DТ наз. средней Т., отношение бесконечно
малых величин dQ/dT-истинной Т. Поскольку dQ не является
полным дифференциалом ф-ции состояния, то и Т. зависит от пути перехода между
двумя состояниями системы. Различают Т. системы в целом (Дж/К), удельную Т.
[Дж/(г·К)], молярную Т. [Дж/(моль·К)]. Во всех ниже приведенных ф-лах использованы
молярные величины Т.
Из второго начала термодинамики
следует, что Т. пропорциональна производной от энтропии системы S по
т-ре Т при постоянстве внеш. силы или термодинамич. координаты (обозначается
индексом z):

Наиб. важными видами Т.
являются Т. CV при постоянном объеме V и Т. Ср
при постоянном давлении р:
СV =
(9U/9T)V = T(9S/9T)V,
Ср = (9Н/9Т)р = Т(9S/9Т)р,
где U-внутр. энергия,
H-энтальпия системы. Значения Ср и СV
связаны соотношением:
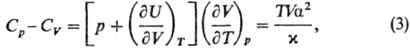
где a = V-1(9V/9Т)р-коэф.
термич. расширения, x = = — V-1(9V/9р)T-коэф.
изотермич. сжимаемости. Поскольку по условиям устойчивости фаз Ср,
CV > 0 и (9V/9р)T
< 0, то согласно (3) Ср > CV. Это естественно,
т. к. при изобарич. нагревании часть тепла, помимо увеличения внутр. энергии
системы, идет на работу расширения. Для идеальных газов (9U/9V)T
= 0 и учет ур-ния состояния pV= RT приводит к соотношению: Сp
- CV = R (R-газовая постоянная). Из определений
(1) и (2) следует, что для изотермич. процесса С = ,,
для адиабатич. процесса С = 0.
Т. газов. Вычисление
Т. сводится к вычислению средней энергии теплового движения отдельных молекул,
к-рое складывается из поступат. и вращат. движений молекулы как целого и из
колебаний атомов внутри молекулы. Молярная Т. одноатомного газа равна 3R/2
(по R/2 на каждую степень поступат. движения молекулы). Т.
многоатомного газа
в общем случае м. б. представлена суммой вкладов от отдельных видов движения-поступательного,
вращательного, колебательного.
Поступательная Т. рассчитывается
так же, как для одноатомного газа. Вращательная и в особенности колебательная
Т. должны, как правило, вычисляться на основе квантовой статистики. Согласно
классич. статистике, вклады в молярную Т. в расчете на одну степень свободы
равны: для вращат. движения R/2, для колебат. движения R. Для
большинства молекул при низких и средних т-рах колебат. степени свободы вырождены
и не дают вклада в Т. Напр., Т. двухатомного газа при обычных т-рах равна 5R/2.
Лишь при достаточно высоких т-рах возбуждаются колебания определенной частоты.
Т. твердых тел. При
низких т-рах Т. одноатомных кристаллов пропорциональна кубу абс. т-ры (закон
Дебая): СV ! Т3. При высоких т-рах
СV стремится к предельному значению 3R, определяемому
классич. теорией и не зависящему от природы атомов (правило Дюлонга и Пти).
Значение 3R может, однако, не достигаться, если ранее происходит плавление
в-ва или его разложение. Методами квантовой статистики доказывается равенство
нулю Т. любого тела при абс. нуле т-ры (CV : 0 при Т : 0). Если бы это было не так, энтропия системы, согласно (2), должна
была бы обращаться в — , при T : 0, что противоречит третьему
началу термодинамики (см. Тепловая теорема
). Предельное значение
СV = 3R достигается уже при обычных т-рах у металлов.
Для нек-рых простых соед. с числом атомов в молекуле n предельное значение
CV = 3nR [NaCl, MnS (n = = 2), РbСl2(n
= 3) и др.].
Для кристаллич. твердых
тел существует характеристич. т-ра qD, названная т-рой
Дебая, разделяющая "классич. область" т-р Т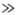 qD,
в к-рой Т. описывается законом Дюлонга и Пти, и "квантовую область"
T
qD,
в к-рой Т. описывается законом Дюлонга и Пти, и "квантовую область"
T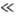 qD.
Т-ра Дебая связана с предельной частотой колебаний атомов в кристал-лич. решетке
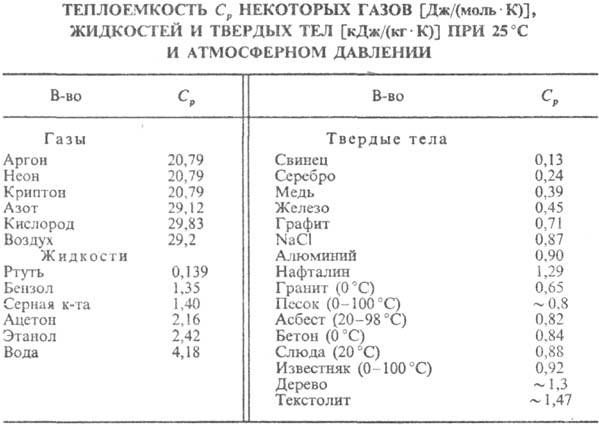
и зависит от упругих постоянных в-ва (см. табл.).
qD.
Т-ра Дебая связана с предельной частотой колебаний атомов в кристал-лич. решетке
и зависит от упругих постоянных в-ва (см. табл.).
У металлов вклад в значение
СV дают электроны проводимости (электронная Т.). Эта часть
Т. может быть вычислена на основе квантовой статистики Ферми, к-рой подчиняются
электроны. Электронная Т. пропорциональна т-ре в первой степени, однако ее вклад
пренебрежимо мал при т-рах, когда велика "решеточная" Т. (пропорциональная
T3). Антиферромагнетики и ферримагнетики, обладающие упорядоченным
расположением спиновых магн. моментов атомов, имеют дополнит. магн. составляющую
Т., к-рая испытывает резкий подъем при т-ре фазового перехода в-ва в парамагнитное
состояние (см. Кюри точка
).
Методы определения Т.
индивидуальных веществ. Осн. эксперим. методом является калориметрия
.
Теоретич. расчет Т. в-в осуществляется методами статистической термодинамики
,
но он возможен только для сравнительно простых молекул в состоянии идеального
газа и для кристаллов, причем в обоих случаях для расчета требуются эксперим.
данные о строении в-ва.
Эмпирич. методы определения
Т. в-в в состоянии идеального газа основаны на представлении об аддитивности
вкладов отдельных групп атомов или хим. связей. Опубликованы обширные таблицы
групповых атомных вкладов в значение Ср. Для жидкостей, помимо
аддитивно-групповых, применяют методы, основанные на соответственных состояний законе
, а также на использовании термодинамич. циклов, позволяющих перейти
к Т. жидкости от Т. идеального газа через температурную производную энтальпии
испарения.
Для р-ра вычисление Т.
как аддитивной ф-ции Т. компонентов в общем случае некорректно, т.к. избыточная
Т. р-ра, как правило, значительна. Для ее оценки требуется привлечение молекулярно-статистич.
теории р-ров (см. Растворы неэлектролитов
). Экспериментально избыточная
Т. может быть определена по температурной зависимости энтальпии смешения, после
чего возможен расчет Ср р-ра.
Т. гетерог. систем представляет
наиб. сложный случай для термодинамич. анализа. На диаграмме состояния
перемещение
вдоль кривой равновесия фаз сопровождается изменением и р, и Т. Если
в процессе нагрева происходит смещение точки фазового равновесия, то это дает
дополнит. вклад в Т., поэтому Т. гетерог. системы не равна сумме Т. составляющих
ее фаз, но превосходит ее. На фазовой диаграмме при переходе от гомог. состояния
к области существования гетерог. системы Т. испытывает скачок (см. Фазовые переходы
).
Практическое значение
исследований Т. важно для расчетов энергетич. балансов процессов в хим.
реакторах и др. аппаратах хим. произ-ва, а также для выбора оптим. теплоносителей.
Эксперим. измерение Т. для разных интервалов т-р-от предельно низких до высоких-является
осн. методом определения термодинамич. св-в в-в. Для расчета энтальпий и энтропии
в-ва (в интервалах от 0 до Г) используют интегралы от Т.:
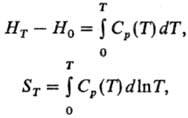
к к-рым добавляютсясоответствующие
эффекты фазовых переходов. Знание Т. реагентов в нек-ром интервале т-р позволяет
осуществить расчет теплового эффекта р-ции (см. Кирхгофа уравнение
),
а знание Т. р-ров-рассчитать их термодинамич. св-ва при любой т-ре в пределах
исследованного интервала.
Особо следует подчеркнуть
роль Т. в структурных исследованиях индивидуальных в-в в конденсир. состоянии
и р-ров. Величины, являющиеся второй производной потенциалов Гиббса или Гельмгольца
по параметрам состояния (а Т. относится к таковым), весьма чувствительны к структурным
изменениям системы. В твердых телах и сплавах при фазовых переходах 2-го рода
типа порядок - беспорядок наблюдаются l-образные скачки Т. В жидкостях
такие скачки имеют место вблизи критич. точек равновесия жидкость-газ и жидкость-жидкость
(см. Критические явления
). В жидкости, напр., при нагр. часть
энергии может идти не на возбуждение новых степеней свободы молекул, а на изменение
потенц. энергии взаимодействующих молекул. Этот вклад наз. "конфигурационной"
Т.; она связана с характером мол. упорядочения в жидкостях и р-рах. В биохимии
политермич. измерения Т. дают информацию о структурных переходах в белках.
Лит.: Рид Р., Праусниц
Дж., Шервуд Т., Свойства газов и жидкостей, пер. с англ., 3 изд., Л., 1982;
Шульц М. М., Филиппов В. К., "Ж. Весе. хим. об-ва им. Д.И. Менделеева",
1982, т. 27, с. 485-94; Панов М.Ю., Белоусов В. П., в сб.: Химия и термодинамика
растворов, в. 5, Л., 1982, с. 56-87; Термодинамические свойства индивидуальных
веществ, под ред. В. П. Глушко, 3
изд., т. 1-4, М., 1978-82; Experimental thermodynamics, ed. by J. P. McCullough,
D. W. Scott, v. 1, N. Y. - L., 1968. M. Ю. Панов.
|

