Химическая энциклопедия

ТЕРМОДИНАМИКА НЕОБРАТИМЫХ ПРОЦЕССОВ (неравновесная термодинамика), изучает общие закономерности поведения систем, не находящихся в состоянии термодинамического равновесия . В таких системах имеют место разнообразные неравновесные процессы (теплопередача, диффузия, электрич. ток, хим. р-ции и т. п.), к-рые являются необратимыми в термодинамич. смысле (см. Обратимые и необратимые процессы ). Согласно ур-нию Клау-зиуса, для неадиабатич. процессов изменение энтропии системы dS равно:

где d_eS = dQ/T- "внешнее" изменение энтропии, связанное с обратимым теплообменом с окружающей средой (dQ-бесконечно малое кол-во теплоты, T-абс. т-ра), d_iS- "внутреннее" изменение энтропии, обусловленное самопроизвольным протеканием в системе необратимых процессов. При этом d_i S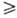О, где знак равенства относится к состоянию равновесия или к случаю обратимых (квазистатич.) процессов. Величина d_iS играет центр. роль в Т. н. п.

К осн. задачам Т. н. п. относят исследование балансов физ. величин (энергии, массы, энтропии и др.) при переходах, превращениях и диссипации энергии, а также установление законов эволюции макроскопич. систем. В этой связи в Т.н.п. появляется и играет важную роль время t-переменная, отсутствующая в равновесной термодинамике (равновесные в термодинамич. смысле процессы протекают бесконечно медленно). Поэтому вместо (1) рассматривается соотношение:

dS/dt = d_eS/dt + d_iS/dt,

где величина P = d_iS/dt наз. глобальным произ-вом энтропии (т.е. относящееся ко всему объему системы).

Различают феноменологическую Т. н. п. и статистич. теорию неравновесных процессов. Феноменологическая Т. н. п., в свою очередь, подразделяется на линейную и нелинейную теории. Обычно в Т. н. п. рассматриваются три типа систем: однородные, прерывные и непрерывные. В однородных системах в любой момент времени интенсивные св-ва (параметры состояния) - т-ра, давление, хим. потенциал - одинаковы по всему объему. Прерывные (вентильные, гетерогенные) системы состоят из двух и более однородных частей, разделенных либо границей раздела фаз, либо вентилем (напр., газы в сосудах, соединенных мембраной или капилляром), так что св-ва меняются скачком при переходе из одной части в другую. Непрерывными наз. системы, интенсивные св-ва к-рых можно считать непрерывными ф-циями координат точки внутри системы (полевых переменных) и времени.

Соотношения, характеризующие процессы переноса массы, энергии, заряда, энтропии и т.д., записываются в виде балансовых ур-ний. Такие ур-ния м. б. записаны как для непрерывных, так и для прерывных систем. В них всегда фигурируют величины двух типов, одни из к-рых трактуются как потоки, другие-как силы. Потоки характеризуют скорость переноса физ. величины (энергии, массы, энтропии и т.д.) через воображаемую единичную площадку или скорость хим. р-ции. Термодинамич. силы-это причины, порождающие потоки. Для процессов переноса в непрерывных системах силы имеют характер градиентов (т-ры, концентрации и т.п.), в прерывных - конечных разностей этих величин.

Неравновесные процессы принято подразделять на скалярные, векторные и тензорные, если потоки и силы являются соотв. скалярами, векторами или тензорами. В зависимости от этого для описания процессов нужно использовать скалярное, векторное поле или поле тензора 2-го ранга. К группе скалярных процессов относят, в частности, хим. р-ции (скорость р-ции в каждой точке внутри системы характеризуется скалярной величиной). К векторным процессам относят, напр., теплопроводность и диффузию (с ними связаны поля векторов потоков тепла и в-ва). Примером тензорного процесса служит вязкое течение. Классификация процессов по тензорным св-вам не является формальной, но связана с содержанием принципа Кюри (см. ниже). Ур-ния балансов массы, импульса, полной энергии имеют смысл законов сохранения. Баланс внутр. энергии суть первое начало термодинамики . Его можно представить в виде ур-ния:

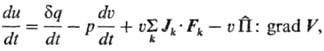
где и, u, q-уд. локальные (относящиеся к нек-рому выделенному элементу объема) внутр. энергия, объем и кол-во тепла соотв.; p -давление; J_k- диффузионный поток k-го компонента в поле внеш. силы F_k, действующей на единицу массы k-го компонента (точка означает скалярное произведение); V-вектор скорости центра масс системы в поле внутр. напряжений; П-тензор вязких напряжений (вязкий тензор давления); 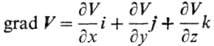(двоеточие означает двукратную свертку). Для невязких систем в поле сил тяготения последние два слагаемых обращаются в нуль, и приведенная формулировка первого начала аналогична формулировкам, принятым в равновесной термодинамике.

Уравнение баланса энтропии имеет наиб. важное значение в Т.н.п., т.к. на его основе определяются потоки и силы. Полная, или субстанциональная, производная энтропии по времени имеет вид ур-ния:

где r-плотность, s-уд. локальная энтропия, J_s-вектор потока энтропии. Величина s = d_is/dt представляет собой локальную скорость возникновения энтропии за счет необратимых процессов, протекающих внутри выделенного элемента объема, и наз. локальным произ-вом энтропии. Положит. знак произ-ва энтропии (s > 0) определяется только необратимыми процессами (напр., диффузией, теплопроводностью, вязкостью). Ур-ние баланса энтропии суть выражение второго начала термодинамики в Т.н.п.

Принцип локального равновесия утверждает, что каждый малый (но макроскопический) элемент объема неравновесной в целом системы в любой момент времени находится в состоянии равновесия. Он базируется на той идее, что малые подсистемы релаксируют к равновесию гораздо быстрее, чем вся система. В рамках феноменологич. теории этот принцип носит характер осн. постулата как в линейной, так и нелинейной Т.н.п., т.к. он позволяет использовать фундам. ур-ния равновесной термодинамики для исследования неравновесных процессов. Так, для малого элемента объема du непрерывной системы можно записать:

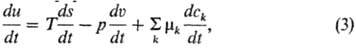
где Т-абс. т-ра, m_k, с_k-хим. потенциал и массовая доля k-го компонента. Ур-ние (3) соответствует фундам. ур-нию Гиб-бса (см. Внутренняя энергия ).

Для изучения неравновесных процессов в Т. н. п. необходимо иметь систему ур-ний, связывающих потоки и силы и основанных на общем термодинамич. подходе. Для этого потоки и силы принято определять таким образом, чтобы произ-во энтропии выражалось стандартной билинейной формой:

где J_i, Х_i-соотв. независимые скалярные потоки и силы, а в случае векторных или тензорных процессов - все декартовы компоненты соответствующих векторных и тензорных величин. Билинейную форму (4) получают подстановкой балансовых ур-ний в соотношение (3) и сопоставлением с ур-нием (2). При этом выбор потоков и сил не является однозначным. Ур-ния выражающие зависимость потоков от сил, наз. термоди-намич. ур-ниями движения или конститутивными ур-ниями.

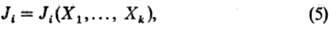
Линейная феноменологическая Т. н. п. принимает в качестве постулата соотношения между потоками и силами вида:

наз. линейными законами Онсагера. Их можно рассматривать как результат разложения потоков J_i в ряд Тейлора по силам X_j вблизи точки равновесия, причем в этом разложении ограничиваются членом первого порядка. Коэффициенты Онсагера L_ij = (9J_i/9x_j)_eq, наз. также кинетич. или феноменологич. коэффициентами, являются ф-циями локальных параметров состояния (т-ры, давления, хим. потенциала и Др.), однако не зависят от потоков и сил, входящих в ур-ния (6). Последнее утверждение, по сути, является еще одним постулатом линейной теории. Зависимости вида (6) хорошо известны из эксперимента; это - пропорциональность силы тока градиенту электрич. потенциала (закон Ома), пропорциональность потока в-ва градиенту концентрации (закон диффузии Фи-ка), пропорциональность потока тепла градиенту т-ры (закон Фурье). В перечисл. примерах потоки возникают под действием "собственных" (сопряженных) сил, чему в (6) соответствуют коэффициенты L_ii. Остальные коэф. L_ij(i . j) описывают т. наз. перекрестные явления, т.е. процессы возникновения потока под действием несопряженной ему силы. Примерами могут служить возникновение потока в-ва под действием градиента т-ры (термодиффузия) и наоборот-потока тепла под действием градиента концентрации (эффект Дюфура), явление термоэлектричества (эффекты Зеебека и Пельтье), электрокинетические явления и др. эффекты. Для мн. перечисл. выше процессов границы применимости линейных законов являются, как показывает опыт, весьма широкими. Это, однако, несправедливо для хим. р-ций, где скорость р-ции ("хим. поток") пропорциональна хим. сродству (сопряженная сила) лишь в непо-средств. близости от хим. равновесия.

На значения кинетич. коэф. L_ij. налагается ряд ограничений, обусловленных тремя независимыми группами причин. Одна группа причин связана с тем, что согласно (4) и (6) локальное произ-во энтропии s в линейной Т. н. п. представляется квадратичной формой:

Положит. определенность произ-ва энтропии (s > 0) приводит, в частности, к след. ограничениям:

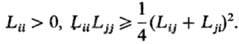
Др. группа ограничений связана с наличием в непрерывной системе элементов пространств. симметрии. Их влияние на характер протекания неравновесных процессов и кинетич. коэф. составляет содержание т. наз. принципа Кюри, согласно к-рому элементами симметрии определяются правила преобразования декартовых компонент потоков и сил при ортогональных преобразованиях координат. Для изотропных систем, вследствие принципа Кюри, не может существовать перекрестных явлений между неравновесными процессами, принадлежащими к разным тензорным группам, т.е. не может возникнуть, напр., под влиянием скалярной силы векторный поток и наоборот. Линейные соотношения могут связывать термодинамич. силы и потоки лишь одинаковой тензорной размерности.

Третья группа ограничений связана с наличием симметрии во времени и носит назв. соотношений взаимности Онсагера. Согласно этим ограничениям, матрица кинетич. коэф. симметрична:

Формально эти соотношения означают, что влияние i-й силы на j-й поток точно Такое же, что и влияние j-й силы на i-й поток. Глубинная же их причина связана с принципом микроскопич. обратимости, являющимся следствием инвариантности законов механики относительно обращения знака времени (см. Детального равновесия принцип ). В виде (8) соотношения взаимности справедливы для тех случаев, когда кинетич. коэф. характеризуют связь потоков и сил одного типа (соотв. четные или нечетные ф-ции) относительно изменения знаков скоростей частиц, образующих систему. В случае потоков и сил разного типа относительно указанной операции справедливы т. наз. соотношения Казимира: L_ij = — L_ji. Соотношения взаимности выведены Л. Онсагером (1931) для скалярных процессов в изолир. систе-мах на основе принципа микроскопич. обратимости, теории флуктуации и линейных законов (теорема Онсагера).

Одной из центр. задач феноменологич. линейной Т.н.п. является вывод замкнутой системы дифференц. ур-ний в частных производных, полностью описывающих поведение непрерывной системы во времени при протекании в ней неравновесных процессов. Поведение сплошной среды можно считать известным макроскопически, если известна зависимость от времени и координат т-ры, плотности, концентрации (массовой доли) в-в и трех компонент вектора центра масс-всего (п + 4) ф-ций для n-компонентной системы.

Замкнутая система ур-ний получается в результате подстановки в балансовые ур-ния вместо потоков их выражении по линейным законам. Из такой системы ур-ний как частные случаи м. б. получены все ур-ния гидродинамики и теплопередачи.

Важные результаты получены в линейной теории при исследовании стационарных состояний. Под стационарным состоянием в Т.н.п. понимается такое состояние системы, к-рое не меняется во времени, но при к-ром, однако, наблюдаются макроскопич. потоки. Условия возникновения стационарных состоянии различны для прерывных и непрерывных систем. Для первых возможно задание и поддержание постоянными внеш. сил, для вторых-лишь задание не зависящих от времени граничных условий. Установлено (И. Пригожин, 1947), что стационарные состояния в прерывных системах при данных внеш. силах, препятствующих достижению равновесного состояния, характеризуются минимумом локального произ-ва энтропии s (теорема Пригожина). В случае непрерывных систем стационарному состоянию отвечает минимум глобального произ-ва энтропии P (принцип миним. произ-ва энтропии):

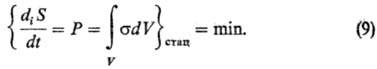
Помимо изложенного выше построения линейной Т. н. п. как локальной полевой теории, существует альтернативный подход, основанный на поисках и использовании вариационных принципов (по аналогии с вариац. принципами механики). Первый такой принцип сформулирован Онсагером (1931) и назван "принципом наименьшего рассеяния энергии". Он м. б. записан в локальной форме (т. е. зависящей от положения элементарного объема) в представлении через потоки:

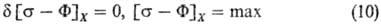
или в представлении через силы:

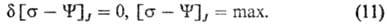
Здесь

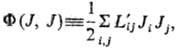
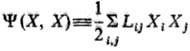
-т. наз. локальные потенциалы рассеяния. При выполнении линейных законов они равны половине локального произ-ва энтропии и так же, как s, являются локальной мерой неравновесности процесса; коэф. L_ij-элементы мат^а рицы, обратной L_ij. В (10) варьирование проводятся по потокам при постоянстве сил, в (11)-наоборот. В обеих формулировках принцип наим. рассеяния энергии эквивалентен линейным ур-ниям и содержит соотношения взаимности Онсагера. И. Дьярмати (1965) сформулировал обобщенный принцип в виде ур-ния: d[s - (Y + F)] = 0, s - (Y + F) = max, где ф-ция [s — (Y + F)] наз. ф-цией Онсагера-Махлупа. В интегральной форме принцип Дьярмати имеет вид:

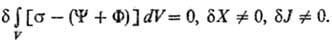
Из вариац. принципов м. б. получены все ур-ния линейной Т. н. п. Упомянутый принцип миним. произ-ва энтропии (9) представляет собой эквивалентную форму принципа миним. рассеяния энергии, записанную в энтропийном представлении применительно к стационарным состоянием. Предложены и др. вариац. принципы Т. н. п. (М. Био, Г. Циглер, Дьярмати, И. Ф. Бахарева).

В настоящее время линейная феноменологическая Т.н.п. является законченной теорией, имеющей очень широкое практич. применение. Процессы диффузии, вязкого течения, теплопередачи должны учитываться при проектировании и анализе режимов работы хим. реакторов и др. аппаратов произ-ва. В хим. термодинамике гетерог. систем с помощью ур-ний линейной Т. н. п. рассчитывают перенос в-ва, заряда, тепла через межфазные границы и переходные слои, в электрохимии-перенос электрич. заряда при разл. условиях (см. Растворы электролитов ). Соотношения Т. н. п. для прерывных систем применяются также при описании мембранных процессов разделения , в т.ч. протекающих с участием биол. мембран. В создание линейной Т. н. п. большой вклад внесли Р. Клаузиус, Т. Де Донде, Онсагер, Пригожий, Дьярмати и др.

Нелинейная Т. в. п. представляет собой развитие теории необратимых процессов применительно к системам, находящимся вдали от термодинамич. равновесия. В нелинейной Т. н. п. сохраняет свое значение основного постулата принцип локального равновесия. Балансовые ур-ния составляются так же, как в линейной Т.н.п. [в частности, локальное произ-во энтропии сохраняет вид (4)], однако связь между потоками и силами носит нелинейный характер, в силу чего перестает быть справедливой ф-ла (7). Типичным примером являются хим. р-ции, поэтому нелинейная Т.н.п. имеет важное значение для хим. и биол. систем.

Поведение систем в нелинейной области имеет ряд принципиальных отличий в сравнении с областью, где действуют линейные соотношения. Во-первых, в системе перестают быть справедливыми соотношения взаимности Онсагера, появляется анизотропия св-в, даже если в равновесном состоянии система изотропна. Во-вторых, в то время как равновесные состояния и стационарные состояния вблизи равновесия описываются в терминах экстремумов нек-рых термодинамич. потенциалов, то в областях, сильно удаленных от равновесия, таких потенциалов найти не удается. В-третьих, если вблизи равновесия описание систем в термодинамике проводится через статистич. средние физ. величины, а флуктуации характеризуют спонтанные отклонения от средних, то вдали от равновесия уже флуктуации определяют значения средних.

Создание совр. нелинейной Т. н. п. в значит. мере является заслугой бельгийской школы физиков во главе с Пригожи-ным. В частности, было установлено, что вдали от равновесия фундаментальной для описания эволюции системы величиной является не произ-во энтропии, а скорость его изменения, точнее та часть скорости изменения произ-ва энтропии d_XP, к-рая связана с изменением термодинамич. сил. Для систем с фиксир. граничными условиями установлено фундам. неравенство:

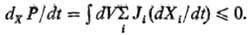
Оно наз. универсальным критерием эволюции" т. к. не требует предложений о характере связи между потоками и силами. Знак равенства отвечает нахождению системы в стационарном состоянии, знак неравенства-эволюции системы к этому состоянию. Важнейшим результатом нелинейной Т.н.п. явилось открытие возможности возникновения в системах, удаленных от равновесия, устойчивых пространственных и временных структур. Эти структуры Наз. диссипативными; им соответствуют те решения дифференц. ур-ний для потоков, к-рые лежат за пределами термодинамич. ветви решений. Диссипативные структуры существуют благодаря обмену энергией и в-вом между системой и окружением (см. Открытая система ). Они характеризуются низкой энтропией, к ним не применим принцип Больцмана, согласно к-рому состояние с большей энтропией более вероятно. Типичный пример временной упорядоченности-возникновение периодич. режимов в го-мог. хим. р-циях (см. Колебательные реакции ).

Т. в. п. и химическая кинетика. Для системы, единств. неравновесным процессом в к-рой является хим. р-ция, конститутивное ур-ниеТ. н. п. имеет вид:

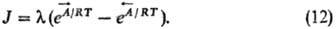
Здесь J - скорость р-ции, 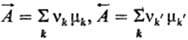- химическое сродство "прямой" и "обратной" р-ций, играющее роль сил; l-коэф., определяемый ф-лой:

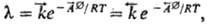
где 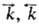- константы скорост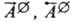и; - стандартные значения сродства. Ур-ние (12) представляет собой действующих масс закон , записанный в форме, позволяющей применять его как к термодинамически идеальным средам (коэф. активности компонентов равны 1), так и к неидеальным (напр., для реальных р-ров); оно наз. ур-нием Марселена - Де Донде. Установлено, что закон действующих масс м.б. выведен из общих принципов Т. н. п.; в частности, форма (12) м. б. получена из обобщенного вариац. принципа Дьярмати. Получение закона действующих масс из принципов Т.н.п. является важным результатом, поскольку тем самым устанавливается взаимное соответствие между двумя областями физ. химии-хим. термодинамикой и хим. кинетикой.

Молекулярно-статистическое обоснование Т.н.п. дает статистич. теория неравновесных процессов. С ее помощью обосновывается принцип локального равновесия и устанавливаются границы его применимости, интерпретируются линейные законы и соотношения взаимности. Статистич. теория позволяет в принципе рассчитывать кикетич. коэф. по мол. данным. В то же время эта теория не обладает такой общностью, как равновесная статистическая термодинамика , поэтому наиб. важные результаты получены для конкретных задач, преим. в теории газов.

Лит.: Пригожин И., Введение в термодинамику необратимых процессов, пер. с англ., М., 1960; Гроот С. де, Мазур П., Неравновесная термодинамика, пер. с англ., М., 1964; Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971; Гленсдорф П., Пригожий И., Термодинамическая теория структуры, устойчивости и флуктуации, пер. с англ., М., 1973; Дьярмати И., Неравновесная термодинамика. Теория поля и вариационные принципы, пер. с англ., М., 1974; Николис Г., Пригожин И., Самоорганизация в неравновесных системах, пер. с англ., М., 1979; Булатов Н.К., Луи-дин А. Б., Термодинамика необратимых физико-химических процессов, М., 1984; Квасников И. А., Термодинамика и статистическая физика. Теория неравновесных систем, М., 1987. М. Ю. Панов.