Химическая энциклопедия

ВАРИАЦИОННЫЙ МЕТОД в квантовой химии, метод приближенного решения ур-ния Шрёдингера [Шредингера] для квантовой системы (атома, молекулы, кристалла). По своей идее близок к мат. методу оценки нек-рой величины из условия максимума или минимума определенной ф-ции (напр., методу наименьших квадратов).

В квантовохим. задачах В. м. обычно определяют волновую ф-цию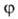 стационарного состояния системы с гамильтонианом Я из условия минимума среднего значения энергии системы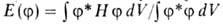 (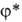-ф-ция, комплексно сопряженная с ср; интегрирование проводится по всей области изменения независимых переменных, описывающих систему). Величина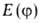 наз. функционалом энергии системы. Согласно т. наз. вариационному принципу, для любой волновой ф-ции выполняется соотношение: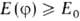, где Е_o- наименьшая энергия системы в стационарном состоянии, т.е. энергия ее осн. состояния. Реально функционал энергии минимизируют в нек-ром ограниченном классе волновых ф-ций, наз. пробными, к-рые выбирают на основе физ. представлений о характере взаимод. частиц в системе. Поэтому если точное решение ур-ния Шрёдингера [Шредингера] получить невозможно, то минимизируя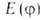 в классе пробных ф-ций, находят волновую ф-цию, к-рая является макс. приближением к точной волновой ф-ции осн. состояния системы, и приближенное значение E_o.

Нахождение минимума этой ф-ции математически выражается условием обращения в нуль вариации:

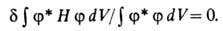
В линейном В.м. (методе Ритца) в кач-ве пробной волновой ф-ции для исследуемой системы принимают линейную комбинацию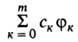 нек-рых разумно выбранных волновых ф-ций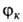. При описании молекулярной системы в качестве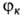 м. 6. выбраны волновые ф-ции, отвечающие разл. валентным схемам (см. Валентных связей метод ), или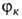 могут описывать отдельные электронные конфигурации системы (см. Молекулярных орбиталей методы ). Коэф. с_к линейной комбинации рассматриваются как переменные параметры системы, функционал энергии - как обычная ф-ция этих параметров. Приближенное решение ур-ния Шрёдингера [Шредингера] проводится в итоге по след. схеме: 1) рассчитывают матричные элементы гамильтониана H_кl =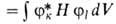 и интегралы перекрывания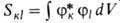 для всех пар ф-ци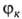й и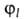и строят матрицы гамильтониана Н и перекрывания S. 2) С помощью этих матриц условие экстремума функционала энергии представляют в форм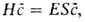е: где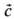-вектор, координаты к-рого - с_к. 3) Находят ненулевые решения этого ур-ния, к-рым отвечает т. наз. вековое уравнение (термин небесной механики) det (Н — — ES) = О (det-символ определителя матрицы). 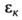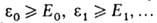Вековое ур-ние имеет (m+1) решений (к = 0, 1, 2, ..., т), к-рые являются оценками сверху для точных значений энергии системы в стационарном состоянии, занумерованных в порядке их возрастания: Возможность получения этих значений энергии в рамках линейного В.м. широко используют для изучения возбужденных состояний молекулярных систем.

Применяют и более сложные варианты В.м. Напр., при исследовании молекулы пробную волновую ф-цию конструируют из орбиталей, характеризующих состояние электрона в молекуле. Это позволяет найти ур-ния, задающие оптимальный набор орбиталей и эффективный потенциал, определяющий состояние электронов в молекуле. В.м. используют также для решения задач теории рассеяния, оценки энергий возбуждения и ионизации и др. Условие надежности расчетов, получаемых В. м., - правильные качеств. представления о природе исследуемого объекта и физически обоснованный выбор класса пробных ф-ций.

Лит.: Эпштейн С., Вариационный метод в квантовой химии, пер. с англ., М., 1977. В. И. Пупышев.