Химическая энциклопедия

ВНУТРЕННЯЯ ЭНЕРГИЯ термодинамич. ф-ция состояния системы, ее энергия, определяемая внутр. состоянием. В.э. складывается в осн. из кинетич. энергии движения частиц (атомов, молекул, ионов, электронов) и энергии взаимод. между ними (внутри- и межмолекулярной). На В.э. влияет изменение внутр. состояния системы под действием внеш. поля; во В.э. входит, в частности, энергия, связанная с поляризацией диэлектрика во внеш. электрич. поле и намагничиванием парамагнетика во внеш. магн. поле. Кинетич. энергия системы как целого и потенциальная энергия, обусловленная пространств. расположением системы, во В.э. не включаются. В термодинамике определяется лишь изменение В. э. в разл. процессах. Поэтому В. э. задают с точностью до нек-рого постоянного слагаемого, зависящего от энергии, принятой за нуль отсчета.

В.э. U как ф-ция состояния вводится первым началом термодинамики , согласно к-рому разность между теплотой Q, переданной системе, и работой W, совершаемой системой, зависит только от начального и конечного состояний системы и не зависит от пути перехода, т.е. представляет изменение ф-ции состояния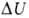

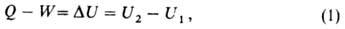
где U₁ и U₂ - В.э. системы в начальном и конечном состояниях соответственно. Ур-ние (1) выражает закон сохранения энергии в применении к термодинамич. процессам, т. е. процессам, в к-рых происходит передача теплоты. Для циклич. процесса, возвращающего систему в начальное состояние,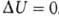 . В изохорных процессах, т.е. процессах при постоянном объеме, система не совершает работы за счет расширения, W=0 и теплота, переданная системе, равна приращению В.э.: Q_v=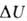. Для адиабатич. процессов, когда Q = 0,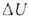 = - W.

В.э. системы как ф-ция ее энтропии S, объема V и числа молей m_i i-того компонента представляет собой термодинамический потенциал . Это является следствием первого и второго начал термодинамики и выражается соотношением:

"

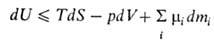где Т - абс. т-ра, р- давление,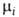-хим. потенциал i-того компонента. Знак равенства относится к равновесным процессам, знак неравенства-к неравновесным. Для системы с заданными значениями S, V, m_i (закрытая система в жесткой адиабатной оболочке) В.э. при равновесии минимальна. Убыль В. э. в обратимых процессах при постоянных V и S равна макс. полезной работе (см. Максимальная работа реакции ).

Зависимость В.э. равновесной системы от т-ры и объема U =f(T, V)наз. калорическим уравнением состояния. Производная В.э. по т-ре при постоянном объеме равна изохорной теплоемкости:

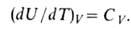
В.э. идеального газа от объема не зависит и определяется только т-рой.

Экспериментально определяют значение В.э. в-ва, отсчитываемое от ее значения при абс. нуле т-ры. Определение В.э. требует данных о теплоемкости С_V(Т), теплотах фазовых переходов, об ур-нии состояния. Изменение В.э. при хим. р-циях (в частности, стандартная В. э. образования в-ва) определяется по данным о тепловых эффектах р-ций, а также по спектральным данным. Теоретич. расчет В. э. осуществляется методами статистич. термодинамики, к-рая определяет В.э. как среднюю энергию системы в заданных условиях изоляции (напр., при заданных Т, V, m_i). В.э. одноатомного идеального газа складывается из средней энергии поступат. движения молекул и средней энергии возбужденных электронных состояний; для двух- и многоатомных газов к этому значению добавляется также средняя энергия вращения молекул и их колебаний около положения равновесия. В.э. 1 моля одноатомного идеального газа при т-рах порядка сотен К составляет 3RT/2, где R-газовая постоянная; она сводится к средней энергии поступат. движения молекул. Для двухатомного газа мольное значение В.э.-ок. 5RT/2 (сумма поступат. и вращат. вкладов). Указанные значения отвечают закону равнораспределения энергии для названных видов движения и вытекают из законов классич. статистич. механики. Расчет колебат. и электронного вкладов во В.э., а также вращат. вклада при низких т-рах требует учета квантовомех. закономерностей. В.э. реальных систем включает помимо вкладов, учитываемых для идеального газа, также среднюю энергию межмолекулярных взаимодействии .

Лит.: Ландау Л. Д., Лифшиц Е. М., Статистическая физика, 2 изд., М., 1964; Полторак О. М., Лекции по химической термодинамике, М., 1971; Ка-рапетьянц М. X., Химическая термодинамика, 3 изд., М., 1975. Н. А. Смирнова.