Химическая энциклопедия

ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ , устанавливает существование энтропии как ф-ции состояния макроскопич. системы и вводит понятие абс. термодинамич. т-ры. Утверждает, что все процессы, протекающие с конечной скоростью, в принципе необратимы, и дает термодинамич. критерии для определения направленности процессов. Вместе с первым началом термодинамики - основа классич., или феноменологич., термодинамики, к-рую можно рассматривать как развитую систему следствий этих двух начал.

Существует неск. разл. формулировок В. н. т. и способов его обоснования, однако все они взаимосвязаны и в конечном счете эквивалентны. В частности, В. н. т. можно формулировать как невозможность создания вечного двигателя второго рода - устройства, в к-ром рабочее тело совершало бы в периодич. цикле работу, находясь в тепловом контакте с одним источником теплоты (В. Оствальд, 1888). Во всех реальных тепловых двигателях превращение теплоты в работу обязательно сопровождается передачей определенного кол-ва теплоты окружающим телам и изменением их термодинамич. состояния, т.е. необратимо. Согласно В. н. т., необратимость того или иного процесса означает, что систему, в к-рой произошел процесс, невозможно вернуть в исходное состояние без к.-л. изменений в окружающей среде. Процессы, допускающие возвращение в исходное состояние как самой системы, так и внеш. среды без к.-л. изменений в них, наз. обратимыми. Обратимы лишь квазистатич. процессы, представляющие собой непрерывную последовательность состояний равновесия и протекающие бесконечно медленно. Все естеств. процессы, происходящие с конечными скоростями, необратимы; они протекают самопроизвольно в одном направлении. Помимо перехода теплоты в работу в циклич. процессах, необратимыми являются, напр., процессы выравнивания т-ры (теплопроводность) или концентрации компонентов системы (диффузия), хим. р-ции.

Согласно наиболее общей формулировке В. н. т., бесконечно малое кол-во тепла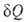, переданное системе в обратимом процессе, отнесенное к абс. т-ре Т, является полным дифференциалом ф-ции состояния 5, наз. энтропией. Для обратимых процессов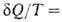 dS; для необратимых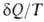 < dS. Для любых процессов (обратимых и необратимых) В. н.т. может быть обобщено записью dS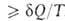 . В изолированных (замкнутых) системах 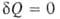и dS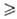0, т.е. возможны лишь процессы, сопровождающиеся увеличением энтропии (закон возрастания энтропии). В состоянии равновесия энтропия изолированной системы достигает максимума и никакие макроскопич. процессы в такой системе невозможны.

Первое начало термодинамики, представляющее собой закон сохранения энергии для систем, в к-рых происходят тепловые и мех. процессы, не позволяет судить об эволюции термодинамич. системы. Значение В.н.т. состоит в том, что оно позволяет выделить фактически возможные в системе процессы из всех допускаемых первым началом и определить состояние термодинамич. равновесия системы, в к-ром никакие макроскопич. процессы без изменения внеш. условий невозможны. Сочетание В.н.т. в форме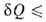TdS с первым началом dU —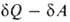, где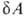-совершенная системой работа, приводит в общем случае необратимых процессов к неравенству: dU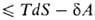. Это неравенство позволяет устанавливать направление протекания самопроизвольных (необратимых) процессов в закрытых системах и критерии равновесия при постоянных значениях любой из пар параметров состояния: Т, р; Т, V; S, р; S, V. Так, в системах, находящихся при постоянных Т и р, процессы самопроизвольно идут в направлении убыли энергии Гиббса G = U + pV— TS, а в состоянии равновесия энергия Гиббса достигает минимума. Это относится, в частности, к хим. р-циям, растворению, изменениям агрегатного состояния и др. превращениям в-в. Последовательное применение В.н.т. к неравновесным системам и протекающим в них необратимым процессам составляет содержание термодинамики необратимых процессов .

Статистич. физика связывает энтропию с вероятностью осуществления данного макроскопич. состояния системы. Для системы из N частиц, обладающей энергией E, энтропия определяется как логарифм статистич. веса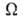данного равновесного состояния: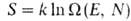 , т.е. числа квантовых состояний в узком интервале 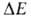вблизи значения Е (k-постоянная Больцмана). Возрастание энтропии изолированной системы обусловлено ее переходом из менее вероятного в более вероятное состояние. Иными словами, эволюция такой системы осуществляется в направлении наиб. вероятного распределения энергии по отдельным частицам или подсистемам (см. Статистическая термодинамика ). Однако вследствие флуктуации, обусловленных хаотич. движением образующих систему частиц, возможен переход системы из более вероятного в менее вероятное состояние; при этом энтропия системы уменьшается. Наличие флуктуации приводит к тому, что закон возрастания энтропии выполняется только в среднем для достаточно большого промежутка времени.

Само название "В. н. т." и исторически первая его формулировка (1850) принадлежат Р. Клаузиусу; последующие формулировки связаны с именами У. Томсона, В. Оствальда, С. Карно, Л. Больцмана. Буквальное применение В. н. т. к Вселенной как целому привело Р. Клаузиуса к ошибочному выводу о неизбежности "тепловой смерти" Вселенной после достижения ею максимума энтропии.

Лит. см. при статьях Статистическая термодинамика . Химическая термодинамика. В. А. Михайлов.