Химическая энциклопедия

БИМОЛЕКУЛЯРНЫЕ РЕАКЦИИ , хим. р-ции, в элементарном акте к-рых превращению подвергаются две частицы (молекулы, радикалы или ионы). В результате могут возникать одна, две или (в редких случаях) три и более частиц продукта:

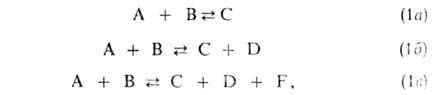
где А и В - молекулы реагентов, С, D и F - молекулы продуктов. Наиб. обширный класс Б.р. - р-ции типа (16). бимолекулярные как в прямом, так и в обратном направлениях. Их кинетика описывается ур-нием:

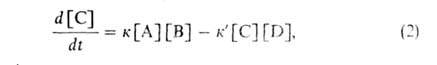
где к и к-константы скорости р-ции соотв. в прямом и обратном направлениях, [А], [В] и [С], [D] - концентрации реагентов и продуктов.

Реакции в газах. Поскольку в газах время между последовательными столкновениями молекул (10^-10 с при нормальных условиях) много больше времени столкновение (10^-12 - 10^-13 с), влияние среды (окружения) проявляется лишь в соударениях реагирующих молекул с молекулами окружения до или после столкновения реагирующих молекул друг с другом, но не за время одного столкновения. Поэтому элементарный акт р-ции можно рассматривать как результат изолированного парного столкновения. Tакие столкновения могут приводить к изменению числа частиц с энергией, превышающей энергию активации р-ции Е, и нарушению максвелл-больцмановского распределения частиц по энергиям их относит. движения и внутр. степеням свободы. В зависимости от соотношения скоростей р-ции и процессов релаксации, восстанавливающих это распределение, различают равновесные и неравновесные Б. р.

Равновесные р-ции протекают сравнительно медленно, максвелл-больцмановское распределение практически сохраняется, и скорость р-ции w м. б. рассчитана в рамках активированного комплекса теории :

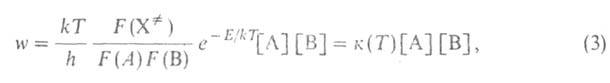
где k и h-постоянные Больцмана и Планка соотв., Т - абс. т-ра, F(A), F(B)и F(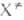)-статистич. суммы исходных реагентов А и В и активированных комплексов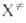, к-т. наз. макроскопич. константа скорости р-ции. Поскольку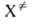 рассматривается как обычная молекула, в к-рой одна степень свободы колебат. движения заменена степенью свободы постулат. движения вдоль координаты р-ции, статистич. сумма F(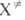) вычисляется как статистич. сумма обычной молекулы без одной степени свободы колебат. движения. Для модели столкновения молекул как жестких шаров с массами m_A и m_B и радиусами r_А и r_B отношение статистич. сумм в (3) равно газокинетич. числу столкновений:

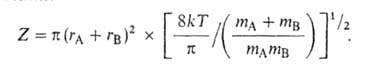
Тогда к(Т)= ZPe^-E/kT, где Р-т. наз. стерич. фактор, учитывающий вероятность наиб. благоприятной для р-ции взаимной ориентации сталкивающихся молекул. Теория активированного комплекса позволяет вычислить его величину в предположении, что при образовании активированного комплекса происходит замена вращат. степеней свободы колебательными. Отсюда следует, что для многих р-ций Р - малая величина (меньше единицы), а их скорость намного меньше значения, рассчитанного на основе газокинетич. теории. Следовательно, стерич. фактор действительно отражает динамич. процессы; в частности, он зависит от вероятности образования предпочтительной для р-ции конфигурации активированного комплекса.

Для неравновесных р-ций, скорость к-рых сравнима со скоростями релаксационных процессов, максвелл-больцмановское распределение нарушается сильно и теория активированного комплекса неприменима. Необходимо учитывать распределения частиц не только по энергиям их относит. движения, но и по квантовым состояниям, а также изменение этих распределений. Для этого стехиометрич. ур-ние (1б)записывают в микроскопич. 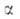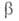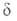форме с учетом фиксированных квантовых состоянийиреагирующих частиц А и В и образующихся из них квантовых состоянийи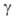 частиц продуктов С и D соотв.:

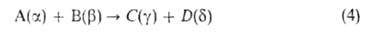
Характеристика такого парного столкновения - т. наз. интегральное сечение р-ции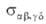 . По физ. смыслу эта величина соответствует площади мишени, центр к-рой совпадает с центром масс одной из реагирующих молекул, если при попадании в эту мишень второй молекулы происходит процесс (4). Произведение скорости относит. движения сталкивающихся частиц на интегральное сечение р-ции равно потоку молекул, к-рые в случае "попадания" в мишень прореагировали или изменили свое квантовое состояние, т.е. равно скорости процесса (4). Теоретич. расчет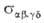 или его эксперим. определение - осн. задача динамики элементарного акта р-ции.

Скорость процесса (4) выражают через сечение р-ции и ф-цию распределения f(и) частиц по скоростям их относит. движения:

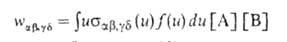
Если бимолекулярный процесс (4) не нарушает термически равновесного распределения частиц по "скоростям, описываемого максвелловской ф-цией f^o(и, Т), он характеризуется т. наз. микроскопич. константой скорости

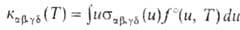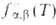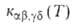. Если же распределение частиц реагентов остается термически равновесным не только по скоростям их относит. движения, но и по внутр. состояниям и характеризуется больцмановской ф-цией представляет интерес полная концентрация частиц продуктов независимо от их квантового состояния. В этом случае р-ция характеризуется макроскопич. константой скорости, к-рую получают из суммированием по конечным состояниям частиц продуктов и усреднением по начальным состояниям частиц реагентов:

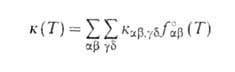
Аналогичным образом м. б. определена любая частично усредненная константа скорости, к-рая описывает кинетику р-ции при разл. степени детализации квантовых состояний частиц реагентов и продуктов.

Т. обр., теория Б. р. связывает кинетич. параметр р-ции — константу скорости к (Т)-с сечением р-ции, т.е. с динамич. характеристикой парного столкновения молекул. Приближенное значение к (Т) для равновесных р-ций может быть также рассчитано в рамках теории активированного комплекса, что позволяет избежать промежут. расчета сечения р-ции и микроскопич. констант скорости.

Для очень быстрых процессов, напр. горения, процессов в ударных волнах и плазме, для ряда космохим. р-ций, когда в системе полностью отсутствует термич. распределение частиц, понятия микроскопич. и макроскопич. констант скорости р-ции теряют смысл и сечение р-ции становится ее единственной характеристикой.

Количеств. оценка скорости Б. р. и расчет констант скорости - чрезвычайно сложная задача, требующая знания ф-ций распределения реагирующих частиц и частиц продуктов по внутр. степеням свободы. Информация о столкновениях между отдельными молекулами на предварительно выбранных энергетич. уровнях стала доступной благодаря использованию молекулярных пучков метода . Для экзотермич. р-ций очень важно исследование ф-ции распределения молекул продуктов по колебательно-вращательным состояниям. Если это распределение сильно неравновесно, запасенная в молекулах энергия м. б. непосредственно превращена в когерентное электромагн. излучение хим. лазера. Другое практич. применение сведений о кинетике неравновесных Б. р. связано с возможностью избирательного увеличения скорости эндотермич. р-ций путем предварительного перевода молекул реагентов в определенные возбужденные состояния . Е.Е. Никитин.

Реакции в жидкостях и твердых телах. Частицы, реагирующие друг с другом в жидкости или в твердом теле, сильно взаимод. с окружением, поэтому ф-ция распределения их по энергии является, как правило, максвелл-больцмановской, а кинетика Б. р.-равновесной. Лимитирующая стадия таких р-ций - собственно хим. взаимод. при контакте реагирующих частиц или диффузионное сближение частиц. В последнем случае скорость р-ции контролируется диффузией, и энергия активации р-ции совпадает с энергией активации диффузии. В твердых телах диффузионное перемещение частиц замедляется настолько, что сближение реакционных центров осуществляется по недиффузионным механизмам: посредством миграции своб. валентности -эстафетной передачей атома Н (в радикальных р-циях), эстафетным переносом протона или электрона, миграцией экситона (в р-циях электронно-возбужденных частиц). Низкая молекулярная подвижность в конденсированной фазе обеспечивает также относительно большое время жизни партнеров-частиц в состоянии контакта и более высокую вероятность р-ции по сравнению с соответствующими газофазными р-циями (см. Клетки эффект ).

Важная особенность Б. р. в жидкостях и твердых телах — сольватация реагентов, к-рая изменяет реакционную способность и состав реагирующих частиц (напр., соотношение своб. и сольватированных радикалов, ионов и ионных пар, молекул и их ассоциатов и т.д.). Сольватация изменяет скорость, а часто и направление и механизм Б. р., влияет на выход продуктов и является поэтому эффективным способом управления р-цией.

Лит.: Термические бимолекулярные реакции в газах, М., 1976; Энтелис С. Г., Тигер Р. П., Кинетика реакций в жидкой фазе, М.. 1973. А. Л. Бучаченко.